是什么让这本教材显得如此出众？这些交互式图表使这本在线教科书独一无二 。交互式插图与文字表述完美锲合 ， 将上下文和视觉辅助应用于定义 ， 定理和示例 。
学习者可以轻松跟随教材 ， 深入了解内容背后的机制 ， 并按照自己的节奏在步骤之间跳跃 。一个很好的例子是交互式插图 9.8 ， 其中作者展示了如何使用线性映射在三维环境中为立方体创建阴影 。

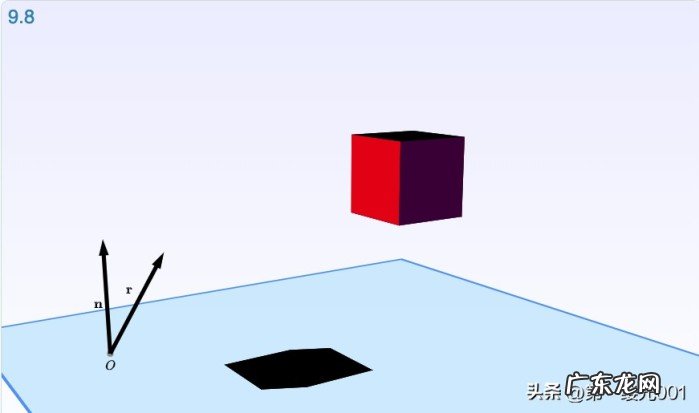
文章插图
?
这本互动教科书的主要优势当然在于它对该领域新手的帮助 。我第一次学习线性代数时 ， 虽然我可以按照模式或步骤去处理证明和习题 ， 但缺乏可视的理解 ， 更多的是依赖机械化演算 。这就是这本教科书的闪光点 。
在这本书的帮助下 ， 初学者将更快地掌握新概念 ， 并提高其背后数学的直觉 。包含定义 ， 定理和证明的原始形式都以清晰和一致的方式编写 。有了这些 ， 丰富而有趣的例子 ， 更能抓住学习者的注意力 。
虽然 immersivemath 并没有重塑我们的学习方式 ， 但它的交互式插图改进了学习者对概念的理解 ， 可以帮助学习者从逻辑上更快地掌握线性代数的基础原理 。我建议任何想学习线性代数的人都应该将这本书作为使用教材之一！
目录

• 前言
• 第 1 章：简介
• 第 2 章：向量
• 第3章 点积
• 第 4 章：向量积
• 第5章 高斯消元
• 第6章：矩阵
• 第7章 行列式
• 第 8 章：秩
• 第 9 章：线性映射
• 第 10 章：特征值和特征向量

• 带你了解上海16个区是如何形成的 上海市有哪几个区
• 夫妻财产过错方是如何分配的
• 如何自制油桶花盆制作方法有哪些
• 长寿花如何长成树养护技巧有哪些
• 真正小叶紫檀树盆景如何养护养护要点有哪些
• 北京汽车托运收费标准 北京汽车托运物流如何收费
• 多杆黄杨盆景如何修剪什么时候修剪比较好
• 盆栽桂花怎么养如何让桂花开花又多又香
• 长春花老桩盆景怎么养如何养才能爆盆
• 工作风水的东西有哪些 如何用风水找工作