也就是r0=1/(2B) 。 同时 ， 根据轨道方程 %u3B8=0的初始位置条件有r0=1/(A+B) 。 结合这两个式子 ， 可知 A=B ， 接着对轨道方程作如下推导：

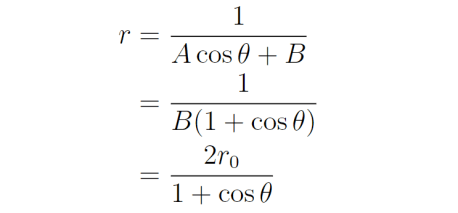
文章图片

张朝阳对这个式子作了进一步解释 ， 初始位置是 %u3B8=0处 ， 带进去就得到r=r0 。 当%u3B8越来越接近 %u3C0， 由于cos(%u3C0)=-1 ， 飞船距离地心的距离r将会趋向于无穷大 。 因此飞船飞到了无穷远处 。 也就是说 ， 飞船逃逸出了地球的引力束缚 。 张朝阳还说到 ， 这时候的轨迹是一条抛物线 。

文章图片

(张朝阳对飞船以第二宇宙速度水平飞出的情况进行讨论)
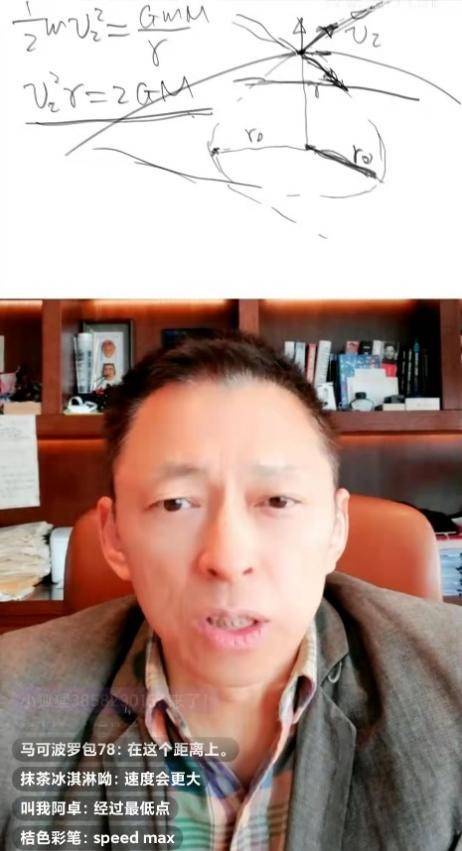
【空间站受到扰动会不会掉下来？张朝阳的物理课继续探讨卫星运动轨道】此外 ， 他还对这个问题作了拓展 ， 假如飞船是斜向上飞出 ， 这时候可以把飞船的轨迹作一下反向延伸 ， 根据能量守恒 ， 在轨迹的近地点处 ， 依然有mv^2/2=GMm/r ， 也就是在近地点处的速度就是相应位置的第二宇宙速度 。
张朝阳解释 ， 第二宇宙速度是一个和距离有关的量 。 在轨迹的近地点处以相应位置的第二宇宙速度飞出就相当于水平以第二宇宙速度飞出 ， 因此飞船是可以逃逸出地球的引力束缚而来到无穷远处的 。 对于飞船是斜向下飞出的情况也类似 ， 只不过因为地球是有大小的 ， 飞船有可能会撞上地球 。 如果没有撞上 ， 它还是可以逃出地球去到无穷远处 。

文章图片

(张朝阳对第二宇宙速度的问题作了拓展)
空间站在碰撞后轨迹会变成椭圆 速度改变量很小时新轨道变化不大
关于空间站受到扰动会不会掉下来的问题 ， 张朝阳采取简化问题突出重点的策略 ， 假设了空间站一开始做的是圆周运动 ， 速度为v0 ， 半径为r0 。 然后在某时刻 ， 空间站碰到一些什么碎片 ， 或者受到太阳风的影响 ， 空间站的速度变成了v0+%u394v ， 速度方向不变 。
根据推导出来的轨迹方程 ， 知道空间站在碰撞后轨迹会变成椭圆 。 因此需要计算出这个椭圆的参数 ， 看看和原来的轨迹相比变化大不大 。 在原来的圆周运动下 ， A0=0 ， r0=1/B0 。 在碰撞后 ， 空间站有了新的轨迹：
张朝阳介绍 ， 因为扰动的瞬间 ， 空间站的位置并没有变化 ， 因此新的轨迹和旧的轨迹必然有重合点 。 又因为扰动没有改变速度方向 ， 因此这个重合点必然在新轨迹的近地点或者远地点处 。 因此有
在这里 ， A可以大于0 ， 也可以小于0 。 大于零就表明此处是近地点 ， 小于零就表明此处是远地点 。
他接着写下了速度在极坐标基矢下的展开式：
借助勾股定理并且代入 %u3B8’=a/r^2 ， 得到:
假如此时飞船受到了微扰 ， 那么速度大小v改变了 ， 同时a也改变了 ， 但是半径不变 。 于是 ， 通过对上式进行微分 ， 有:
由于假设改变的只是速度大小而非方向 ， 再加上原来的速度方向是沿着地球切向的 ， 因此上式右边第一项为0 ， 如此可得到:
根据B=GM/a^2 ， 也就是Ba^2=GM是个常数 ， 有:
结合前面倒数第二个式子 ， 可以得到:
又因为r0=1/B0=1/(A+B) ， 也就是A+B=B0 ， 所以:
于是得到：
将这个结果代回轨迹方程 ， 最终得到:
这就是扰动后的轨道方程 。 张朝阳还做了进一步的解释 ， 当 %u394v大于零时 ， 扰动位置将成为新轨道的近地点；当 %u394v小于零时 ， 扰动位置将成为新轨道的远地点 。 并且 ， 当速度的改变量很小时 ， 新轨道相比于原来的轨道只改变了一点点 ， 因此空间站并不会掉下来 。