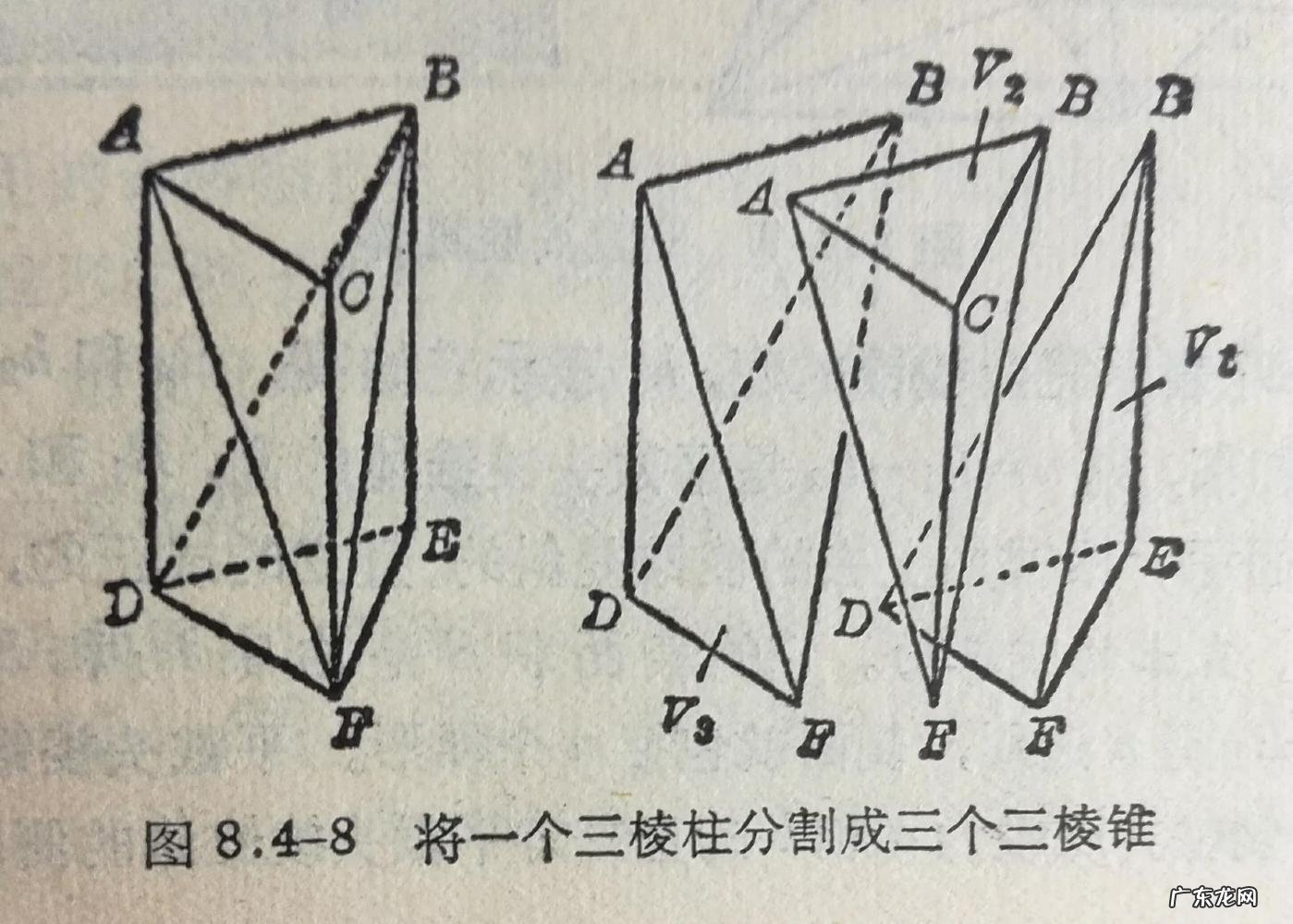
圆锥的体积计算公式圆锥的体积公式推导过程小学( 二 ) _学生

三棱柱体积很好计算，底面积是一个三角形面积，乘以高就得到体积了。三棱锥呢？请看下图：

文章插图

切分三棱柱
一块三棱柱蛋糕可以用刀如图切成三个全等的三棱锥，于是得到下面的结论：
三棱锥的体积是同底同高的棱柱体积的1/3 。
而且还可以此类推，金字塔的体积是同底同高的长方体体积的1/3 。还可以继续以此类推，底面是正多边形的正棱锥体积是同底同高的正多边形柱体体积的1/3 。
为什么呢？因为正多边形可以分为几个全等三角形啊。
再继续推理，得到结论：
圆锥的体积等于同底同高的圆柱体积的1/3 。
这又是什么道理呢？
有两种解释，先说第一种。
我们知道。圆锥和同底同高的圆柱体积之间有数量关系。我们暂时还不知道这个体积比是多少，就假设他们之间的比例为k 。
圆锥体体积：圆柱体体积=kπr2h：πr2h=k
六年级小学生知道比和比例，也会化简比。所以把这个比化简为：
圆锥体体积：圆柱体体积=kr2h：r2h=k
小学生都能看懂。相当于一个分数，分子和分母都同时乘以π的倒数，就消去π了。
我们知道，与圆有关的公式有π ，把π消去再一看，这不是变成底面是正方形的长方体体积公式了吗？
而前面我们已经论述了三棱锥的体积是同底同高的棱柱体积的1/3 ，所以现在我们知道k=1/3 。
于是得到了圆锥体体积公式：
V=1/3 πr2h
现在我们用第二种方法来解释以此类推的数学原理。
伟大的原理：祖暅原理这要从祖暅原理或者是卡瓦列里原理说起。
祖暅原理，又名等幂等积定理，内容是：夹在两个平行平面间的两个几何体，被平行于这两个平行平面的任何平面所截，如果截得两个截面的面积总相等，那么这两个几何体的体积相等。祖暅之《缀术》有云：“缘幂势既同，则积不容异。
在西方，直到17世纪，才由意大利数学家卡瓦列里（Cavalieri.B,1589-1647)于1635年出版的《连续不可分几何》中，提出了等积原理，所以西方人把它称之为“卡瓦列里原理” 。其实，他的发现要比我国的祖暅晚1100多年。
祖暅[gèng]（456年—536年），一作祖暅之，字景烁，范阳遒县（今河北涞水）人。中国南北朝时期数学家、天文学家，祖冲之之子。同父亲祖冲之一起圆满解决了球体积的计算问题，得到正确的体积公式，并据此提出了著名的“祖暅原理” 。
小学数学课堂如何讲解祖暅原理？最简单的方法是用若干本一模一样的书摞在一起，形象化演示。
祖暅原理告诉我们：等底同高的棱锥体积相等。祖暅原理只要求平行截面的面积相等，不要求这些截面的形状相同。所以，根据祖暅原理，同底同高的圆锥体和金字塔体积相等，从前面的论述知道，同底同高的圆锥体与圆柱体体积之比为1:3 。
还有没有别的方法证明圆锥体体积公式呢？请看相关链接：【怎样计算直角三角形重心到直角边的距离？ - 今日头条】https://m.toutiao.com/is/eAFR1a3/
这个链接告诉我们，怎样用帕波斯定理计算旋转体体积，推导出旋转体体积公式。虽然有一定的难度，但是这才是学习数学的正确姿势之一。
祖暅原理威力巨大，掌握了它，解决球体体积也不是难事。
思维拓展：球体体积公式的推导现在，我们可以走得更远，推导出球体体积公式。按照一贯的转化的数学思想，我们考虑一下怎么降低问题的难度。球体不好算，就先考虑半球是什么情况。请看下图：

特别声明：本站内容均来自网友提供或互联网，仅供参考，请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系，我们将在24小时内删除。

圆锥的体积计算公式 圆锥的体积公式推导过程小学( 二 )

圆锥的体积计算公式圆锥的体积公式推导过程小学( 二 )