2002年google工程师们利用贝叶斯网络建立了文章、关键词和概念之间的联系 , 将上百万关键词聚合成若干概念的聚类 , 称之为phil cluster 。 最早的应用是广告的拓展匹配 。
实际上我觉得这个应用他讲的并不清楚 , 我是理解不好 。不如借用《算法杂货铺——分类算法之贝叶斯网络(Bayesian networks)》中的例子说明一下 。
SNS社区中不真实账号的检测
在那个朴素贝叶斯分类器的解决方案中 , 我做了如下假设:SNS社区中不真实账号检测模型中存在四个随机变量:账号真实性R , 头像真实性H , 日志密度L , 好友密度F 。 其中H , L , F是可以观察到的值 , 而我们最关心的R是无法直接观察的 。 这个问题就划归为通过H , L , F的观察值对R进行概率推理 。 推理过程可以如下表示:
i、真实账号比非真实账号平均具有更大的日志密度、更大的好友密度以及更多的使用真实头像 。
ii、日志密度、好友密度和是否使用真实头像在账号真实性给定的条件下是独立的 。
但是 , 上述第二条假设很可能并不成立 。 一般来说 , 好友密度除了与账号是否真实有关 , 还与是否有真实头像有关 , 因为真实的头像会吸引更多人加其为好友 。 因此 , 我们为了获取更准确的分类 , 可以将假设修改如下:
i、真实账号比非真实账号平均具有更大的日志密度、更大的好友密度以及更多的使用真实头像 。
ii、日志密度与好友密度、日志密度与是否使用真实头像在账号真实性给定的条件下是独立的 。
iii、使用真实头像的用户比使用非真实头像的用户平均有更大的好友密度 。
上述假设更接近实际情况 , 但问题随之也来了 , 由于特征属性间存在依赖关系 , 使得朴素贝叶斯分类不适用了 。 既然这样 , 我去寻找另外的解决方案 。
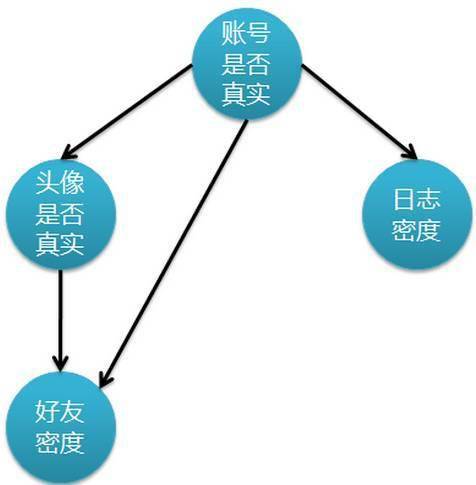
下图表示特征属性之间的关联:
文章图片
上图是一个有向无环图 , 其中每个节点代表一个随机变量 , 而弧则表示两个随机变量之间的联系 , 表示指向结点影响被指向结点 。 不过仅有这个图的话 , 只能定性给出随机变量间的关系 , 如果要定量 , 还需要一些数据 , 这些数据就是每个节点对其直接前驱节点的条件概率 , 而没有前驱节点的节点则使用先验概率表示 。
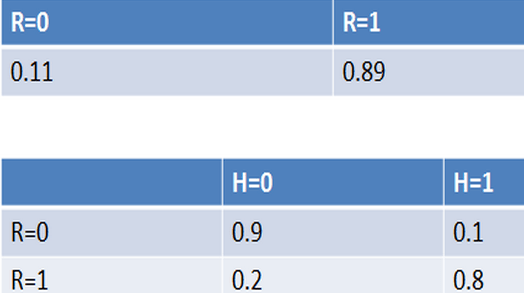
例如 , 通过对训练数据集的统计 , 得到下表(R表示账号真实性 , H表示头像真实性):
文章图片
纵向表头表示条件变量 , 横向表头表示随机变量 。 上表为真实账号和非真实账号的概率 , 而下表为头像真实性对于账号真实性的概率 。 这两张表分别为“账号是否真实”和“头像是否真实”的条件概率表 。 有了这些数据 , 不但能顺向推断 , 还能通过贝叶斯定理进行逆向推断 。 例如 , 现随机抽取一个账户 , 已知其头像为假 , 求其账号也为假的概率:
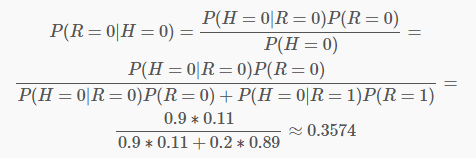
文章图片
也就是说 , 在仅知道头像为假的情况下 , 有大约35.7%的概率此账户也为假 。 如果觉得阅读上述推导有困难 , 请复习概率论中的条件概率、贝叶斯定理及全概率公式 。 如果给出所有节点的条件概率表 , 则可以在观察值不完备的情况下对任意随机变量进行统计推断 。 上述方法就是使用了贝叶斯网络 。
- 使用观察值实例化H,L和F , 把随机值赋给R 。
特别声明:本站内容均来自网友提供或互联网,仅供参考,请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系,我们将在24小时内删除。
