中考数学总复习( 三 )

文章插图

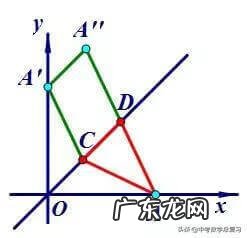
【三角变换类】典型问题：“胡不归” 。
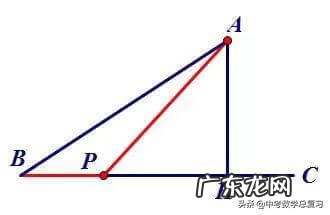
例8.如图，A地在公路BC旁的沙漠里，A到BC的距离AH＝2√3，AB＝2√19，在公路BC上行进的速度是在沙漠里行驶速度的2倍。某人在B地工作，A地家中父亲病危，他急着沿直线BA赶路，谁知最终没能见到父亲最后一面，其父离世之时思念儿子，连连问：“胡不归，胡不归……！”（怎么还不回来），这真是一个悲伤的故事，也是因为不懂数学而导致的。那么，从B至A怎样行进才能最快到达？

文章插图

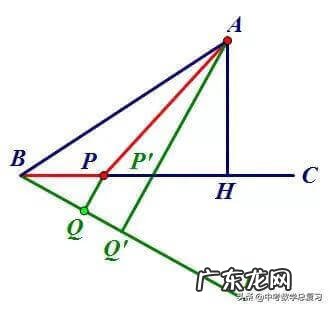
简析：BP段行驶速度是AP段的2倍，要求时间最短即求BP/2+AP最小，从而考虑BP/2如何转化，可以构造含30°角利用三角函数关系把BP/2转化为另一条线段。如下图，作∠CBD=30°，PQ⊥BD，得PQ=1/2BP，由“垂线段最短”知当A、P、Q共线时AP+PQ＝AQ\'最小。

文章插图

【相似变换类】典型问题：“阿氏圆” 。
“阿氏圆”：知平面上两点A、B，则所有满足PA/PB=k且不等于1的点P的轨迹是一个圆，这个轨迹最先由古希腊数学家阿波罗尼斯发现，故称阿氏圆，如下图所示，其中PO：BO＝AO：PO＝PA：PB＝k 。

文章插图

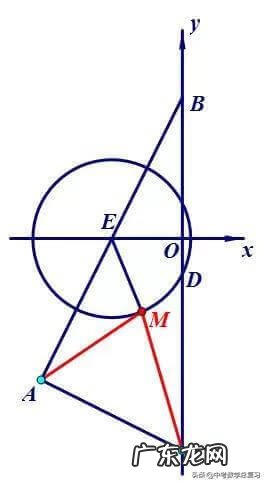
例9.已知A(-4，-4)、B(0, 4)、C(0, -6)、 D(0, -1)，AB与x轴交于点E，以点E为圆心，ED长为半径作圆，点M为⊙E上一动点，求 1/2AM+CM 的最小值。

文章插图

简析：本题的主要问题在于如何转化1/2AM，注意到由条件知在M的运动过程中，EM：AE＝1：2保持不变，从而想到构造相似三角形，使之与△AEM的相似比为1：2，这样便可实现1/2AM的转化，如下图取EN：EM＝1：2，即可得△EMN∽△EAM，再得MN=1/2AM，显然，MN+CM的最小值就是定点N、C之间的最短路径。

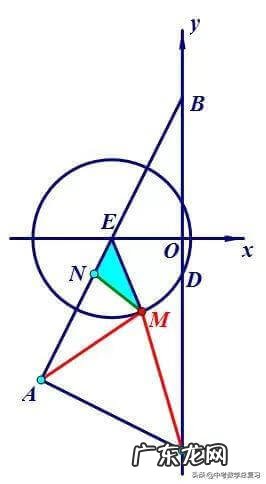
文章插图

之后便是常规方法先求N点坐标，再求CN的长。

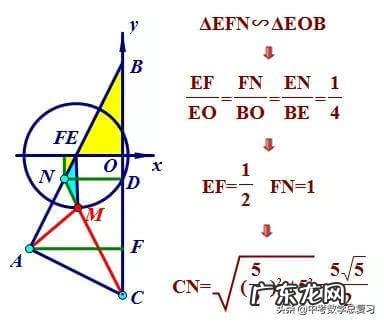
文章插图

【解法大一统】
万法归宗：路径成最短，折线到直线。
（所求路径在一般情况下是若干折线的组合，这些折线在同一直线上时即为最短路径）
基本图形：动点有轨迹，动线居两边。
（动点轨迹可以是线或圆，动线指动点与定点或定线、定圆的连线，动线与折线同指）
核心方法：同侧变异侧，分散化连续。
（动线在同侧进，要变为异侧，一般用翻折、三角、相似的方法构造；动折线被定长线段分散时需化为连续折线，一般用平移的方法构造，如造桥选址问题）
下图是构造完成的目标图形：

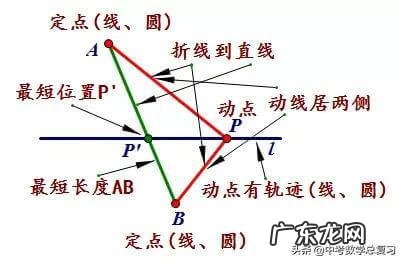
文章插图

再举2例说明上述规律的运用方法：
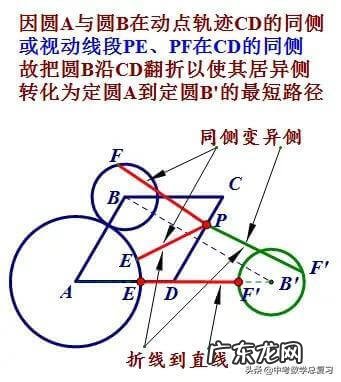
1.如图，菱形ABCD中，∠A=60°，AB＝3，⊙A、⊙B的半径为2和1，P、E、F分别是CD、⊙A、⊙B上的动点，则PE+PF的最小值为。

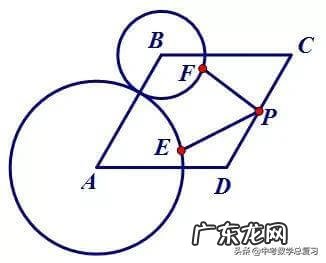
文章插图

思考方法如下图所示：

文章插图

2.菱形ABCD中，∠BAC=60°，P是AC上的动点，求BP+1/2AP的最小值。

特别声明：本站内容均来自网友提供或互联网，仅供参考，请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系，我们将在24小时内删除。