文章图片

在讨论更复杂的模型之前 ， 考虑零层（zero layer）transformer 很有用 。 这类模型接受一个 token ， 嵌入 ， 再取消嵌入 ， 以生成预测下一个 token 的 logits
由于这类模型无法从其他 tokens 传输信息 ， 因此只能从当前 token 预测下一个 token 。 这意味着 ， W_UW_E 的最优行为是近似二元对数似然 。

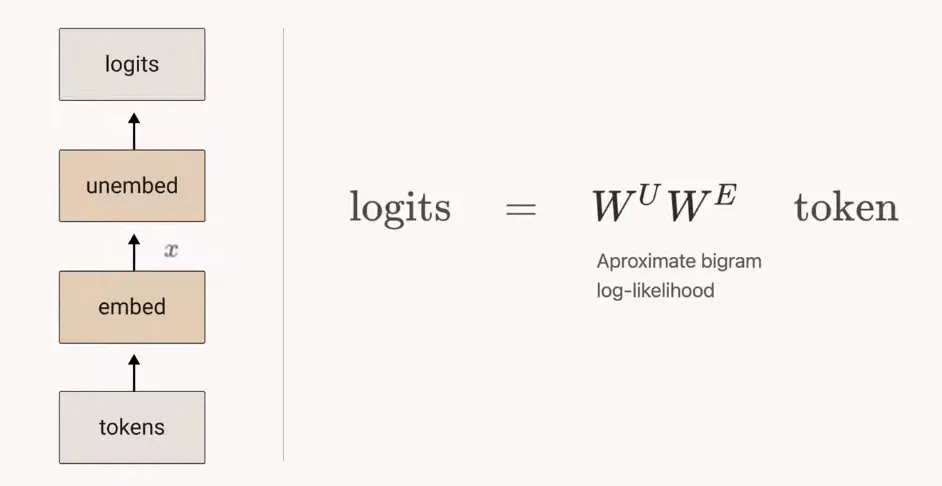
文章图片

零层 attention-only transformers 模型 。
其次 ， 单层 attention-only transformers 是二元和 skip 三元模型的集合 。 同零层 transformers 一样 ， 二元和 skip 三元表可以直接通过权重访问 ， 无需运行模型 。 这些 skip 三元模型的表达能力惊人 ， 包括实现一种非常简单的上下文内学习 。
对于单层 attention-only transformers 模型 ， 有哪些路径扩展（path expansion）技巧呢？研究者提供了一些 。
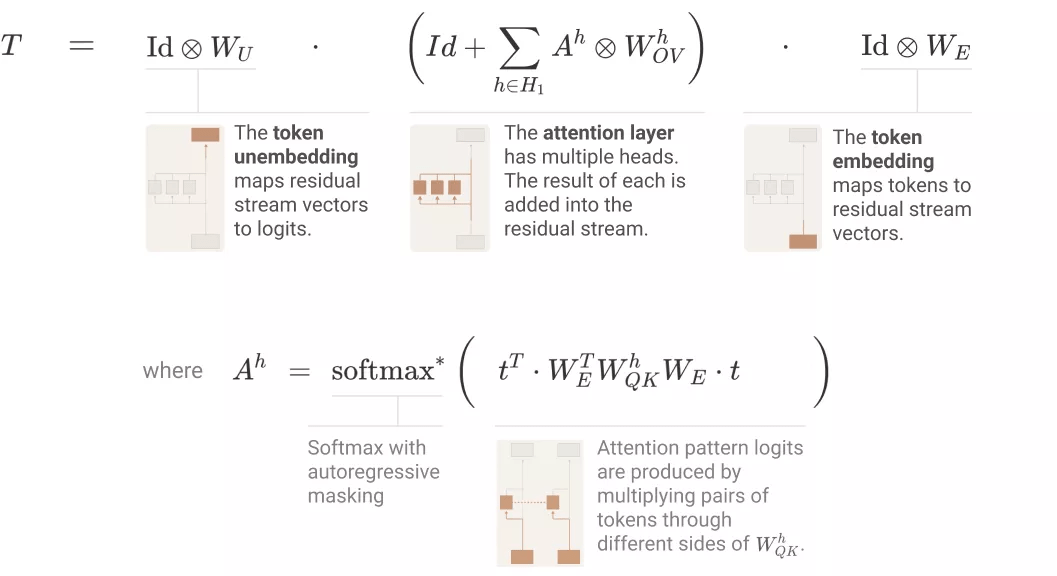
如下图所示 ， 单层 attention-only transformers 由一个 token 嵌入组成 ， 后接一个注意力层（单独应用注意力头） ， 最后是解除嵌入：

文章图片

使用之前得到的张量标记（tensor notation）和注意力头的替代表征 ， 研究者可以将 transformer 表征为三个项的乘积 ， 具体如下图所示：

文章图片

研究者采用的核心技巧是简单地扩展乘积 ， 即将乘积（每个项对应一个层）转换为一个和 ， 其中每个项对应一个端到端路径 。 他们表示 ， 每个端到端路径项都易于理解 ， 可以独立地进行推理 ， 并能够叠加组合创建模型行为 。

文章图片

最后 ， 两层 attention-only transformers 模型可以使用注意力头组合实现复杂得多的算法 。 这些组合算法也可以直接通过权重检测出来 。 需要注意的是 ， 两层模型适应注意力头组合创建「归纳头」（induction heads） ， 这是一种非常通用的上下文内学习算法 。
具体地 ， 当注意力头有以下三种组合选择：

• Q - 组合：W_Q 在一个受前面头影响的子空间中读取；
• K - 组合：W_K 在一个受前面头影响的子空间中读取；
• V - 组合：W_V 在一个受前面头影响的子空间中读取 。

研究者表示 ， Q - 和 K - 组合与 V - 组合截然不同 。 前两者都对注意力模式产生影响 ， 允许注意力头表达复杂得多的模式 。 而 V - 组合对一个注意力头专注于某个给定位置时所要传输的信息产生影响 。 结果是 ， V - 组合头变现得更像一个单一单元 ， 并可以考虑用来创建额外的「虚拟注意力头」 。
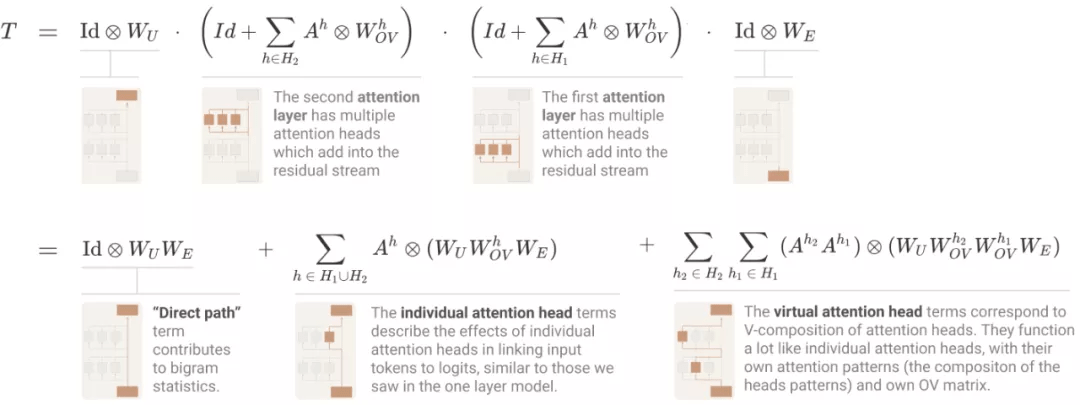
对于 transformer 有一个最基础的问题 ， 即「如何计算 logits」？与单层模型使用的方法一样 ， 研究者写出了一个乘积 ， 其中每个项在模型中都是一个层 ， 并扩展以创建一个和 ， 其中每个项在模型中都是一个端到端路径 。

文章图片

其中 ， 直接路径项和单个头项与单层模型中的相同 。 最后的「虚拟注意力头」项对应于 V - 组合 。 虚拟注意力头在概念上非常有趣 ， 但在实践中 ， 研究者发现它们往往无法在小规模的两层模型中发挥重大作用 。
【经逆向工程，Transformer「翻译」成数学框架 | 25位学者撰文】此外 ， 这些项中的每一个都对应于模型可以实现更复杂注意力模式的一种方式 。 在理论上 ， 很难对它们进行推理 。 但当讨论到归纳头时 ， 会很快在具体实例中用到它们 。