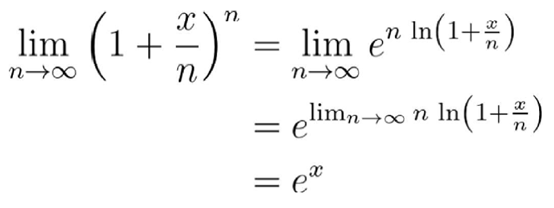
文章图片

最一个简单的替换 ， 就得到了下面这个等价的形式：

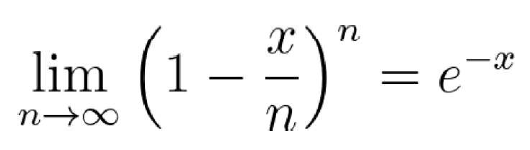
文章图片

现在我们就可以在Γ(z)的定义中运用这个结果 。

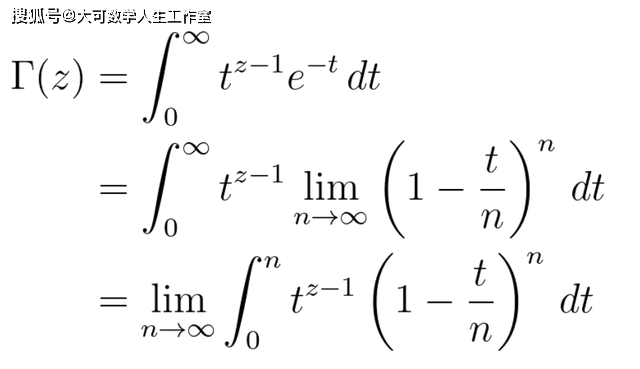
文章图片

把极限符号右侧的积分记作I(n,z) 。
多次运用分部积分 ， 我们得到：

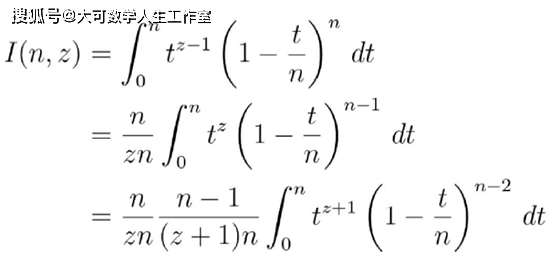
文章图片

继续这种模式 ， 最终消掉了1-t/n的指数项 ， 我们整合一下就得到：

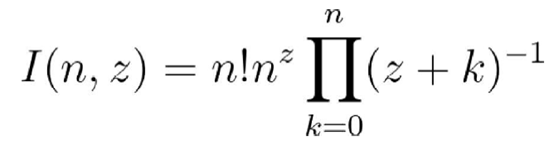
文章图片

为了得到Γ(z) ， 取极限

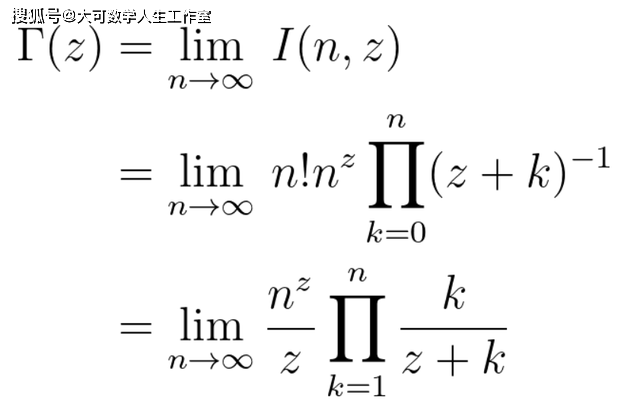
文章图片

这本身已经是一个非常nice ， 并且很著名的结果了 。 但我们不想就此打住 。
我们对这个极限继续做一些简单的操作：

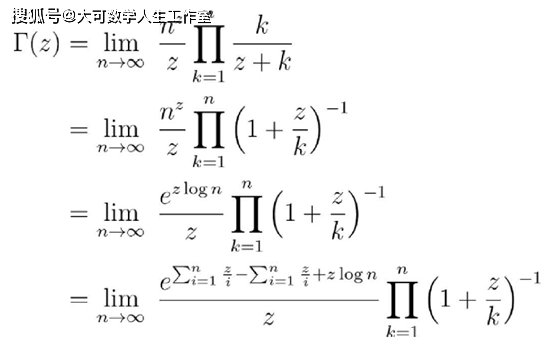
文章图片

这里 ， 我们在e的指数上加上和减去了Σz/i ， 这里的log仍是自然对数 。
我们现在可以将指数化成多项的乘积：

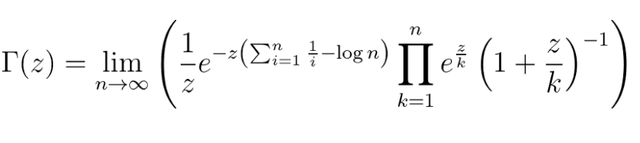
文章图片

回忆一下欧拉常数的定义：

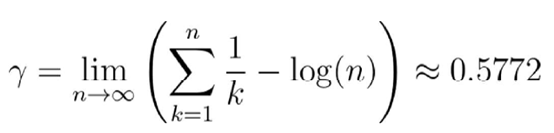
文章图片

若对上面Gamma函数的表达式取极限 ， 我们就得到一个美丽的结果 ， 叫做Gamma函数的Weierstrass积 。

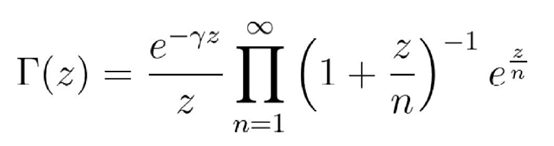
文章图片

看 ， 这是一颗数学的珍珠呢！在某种程度上 ， 这是Gamma函数的一个更好的表达式 ， 我们过会儿再回来 。

文章图片

欧拉的反射公式
数学中最美丽的关系式得益于欧拉 。 不过这次我说的不是他著名的欧拉恒等式 ， 而是反射公式 。 欧拉发现了下面这个令人惊奇的结果 ， 将Gamma函数与三角函数联系了起来 。

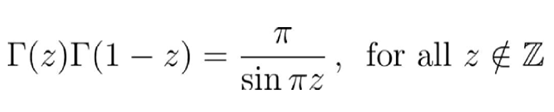
文章图片

证明如下：
顺便提一句 ， sin函数的无穷积也是欧拉发现的！

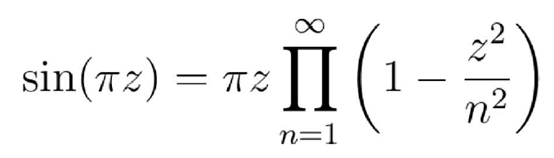
文章图片

如果想看他的证明 ， 你可以去读他的文章《Infinity in Numbers》
Gamma函数的Weierstrass积可以写成

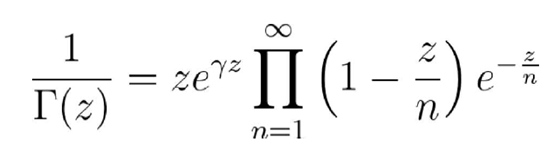
文章图片

通过比较Γ(z)和Γ(-z)我们就能得到：

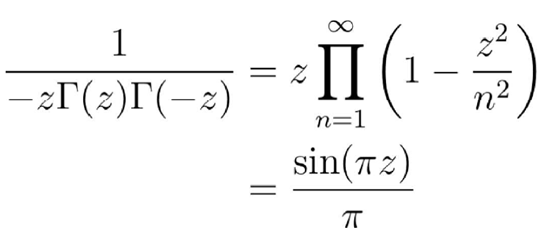
文章图片

然后我们可以运用Gamma函数的函数方程Γ(1-z)= -zΓ(-z)来导出：

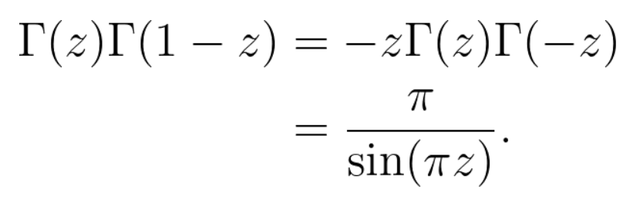
文章图片

很明显z不可为整数 ， 否则分母为0 。
Gamma函数的应用
Gamma函数在数学中可谓无处不在 。 从统计学、数论、复分析 ， 到物理中的弦理论 。 Gamma函数就像把不同领域粘合起来的数学胶水 。 接下来我们将会看到 ， 其实有个非常好的理由解释这一点 。