最后把它写成相应的实部和虚部的形式(使用举世闻名的欧拉恒等式) ， 并考虑这两个公式都隐藏在符号里 。

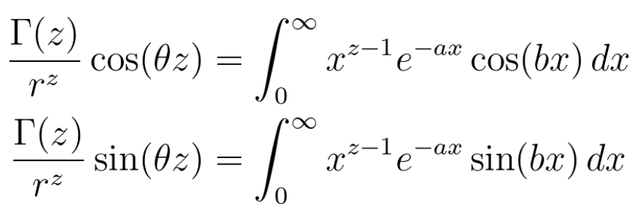
文章图片

这些公式具有难以置信的美 。
注意他们是Gamma函数的推广 ， 因为当w=1时 ， 我们可以从余弦积分方程得到Gamma函数的定义 。
接下来 ， 我们将使用欧拉积分去求解Dirichlet积分 。
Dirichlet积分的推广

文章图片

狄利克雷（Dirichlet）
这是一个有趣的问题 。 方程式如下：

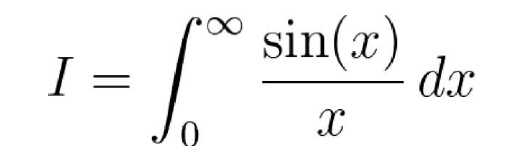
文章图片

这也是一个非常著名的问题 ， 并且有很多方法去求解它 。 比如拉普拉斯变换 ， 双重积分 ， 甚至费曼路径积分！
我们试着从欧拉公式来推导Dirichlet积分 。 事实上 ， 我们将把这一问题推广到更为广泛的结果 ， Dirichlet积分只是一个特殊的结果 。 为了实现这一目的 ， 我们先使用欧拉对称公式去重写sin函数的左边 。 然而 ， 在我们回顾微积分之前 ， 我们可以用洛必达法则来证明

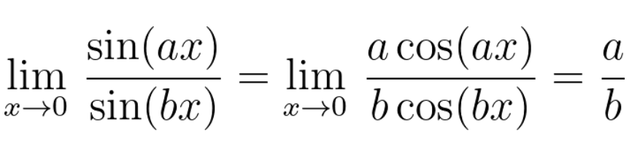
文章图片

我们对欧拉正弦积分公式的左边做一点变换 ，

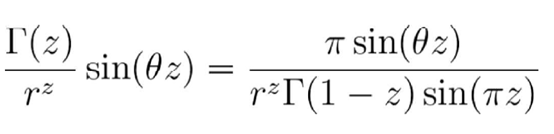
文章图片

根据上面的计算 ， 我们知道

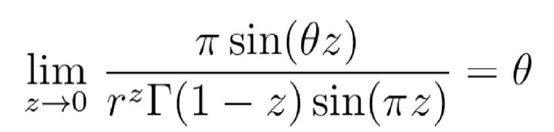
文章图片

当-π<θ<π ,我们有

文章图片

因此 ， 通过对右边取极限 ， 我们得到：

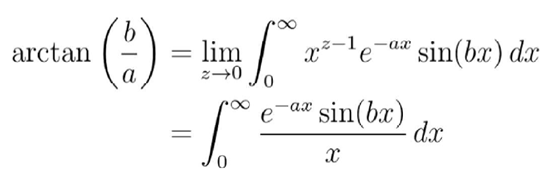
文章图片

这是一个相当好的公式 。

文章图片

注意 ， 当a趋向于0时 ， 那么在方程右边所有b不等于0的实数都将趋于π/2 ， 也就是说 ， 以下观点成立：

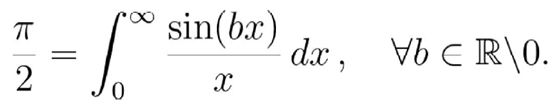
文章图片

在特殊情况下w=i将解出Dirichlet积分 ， 因为此时a=0,b=1 。 所以Dirichlet积分I=π/2 。
什么是(1/2)！？
让我们回到开头的问题 。 当Γ(n+1)=n!对于所有的非负整数n ， 我们可以通过计算使(1/2)！具有意义 。 但是我们怎么做呢？首先 ， 通过方程Γ(z+1)=zΓ(z)将这一问题进行简化 。 因为Γ(3/2)=1/2Γ(1/2) ， 因此只需要找到Γ(1/2)就足够了 。
在z=1/2时 ， 再次使用欧拉的反射公式：

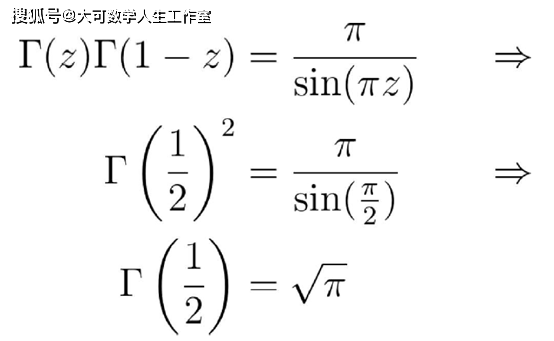
文章图片

因此 ， 我们可以得到：

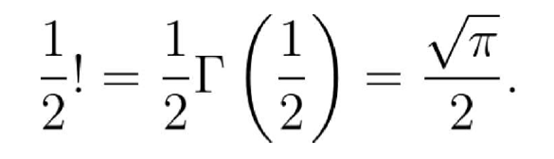
文章图片

结果就显而易见了 。

文章图片

现在让我再来问你一遍：你最喜欢的函数是什么？
作者：Kasper Müller