法线是与函数曲线相切并垂直于切线的直线 。其斜率可通过求函数曲线在该点处的导数（即切线的斜率）后取其相反数得到 。具体步骤如下：
1.求函数曲线在点P的导数 。
2.计算导数f’(x)在点P的函数值，即切线的斜率 。
3.将切线的斜率取相反数，得到法线的斜率 。
注：若函数曲线方程表达式中包含多个变量，则需先将其中除所要求的变量以外的变量当作常数处理，然后再求导 。
切线方程斜率为0法线方程怎么求切线方程公式为：记曲线为y=f(x)则在点(a,f(a))处的切线方程为：y=f'(a)(x-a)+f(a)，法线方程公式：α*β=-1 。
函数图形在某点(a,b)的切线方程y=kx+b:
先求斜率k，等于该点函数的导数值；
再用该点的坐标值代入求b；
切线方程求毕；
法线方程
y=mx+c
m=一1/k；k为切线斜率
再把切点坐标代入求得c 。

文章插图
法线方程导数的求导法则
由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导 。基本的求导法则如下：
1、求导的线性：对函数的线性组合求导，等于先对其中每个部分求导后再取线性组合 。
2、两个函数的乘积的导函数：一导乘二+一乘二导 。
3、两个函数的商的导函数也是一个分式：（子导乘母-子乘母导）除以母平方 。
4、如果有复合函数，则用链式法则求导 。
知道法向量怎么求斜率直线的法向量为n=(a，b)
则直线的斜率为
k=-a/b
【解析】
法线斜率为
【如何法线斜率,切线方程斜率为0法线方程怎么】k法=b/a
法线与已知直线垂直，
∴k=-1/k法=-a/b

文章插图
法线的斜率怎么求切线的斜率是曲线在该点的导数 f '(x0),法线的斜率 k = - 1 / f '(x0).

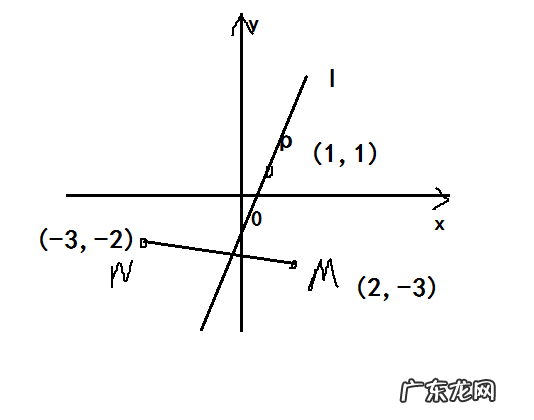
文章插图
法线斜率是什么意思法线斜率是指垂直于曲线上一点的切线的直线的斜率，法线斜率与切线斜率乘积为-1，即若法线斜率和切线斜率分别用α、β表示，则必有α*β=-1 。法线可以用一元一次方程来表示，即法线方程 。与导数有直接的转换关系 。
用导数表示曲线y=f(x)在点M（x0，y0）处的切线方程为：y-f(x0)=f'（x0）（x0-y0）法线方程为：y-f（x0）=(-1/f'（x0）)*（x-x0） 。

文章插图
以下是法线计算方式的相关介绍：
对于像三角形这样的多边形来说 ， 多边形两条相互不平行的边的叉积就是多边形的法线 。用方程ax+by+cz=d表示的平面 ， 向量（a，b，c）就是该平面的法向量 。
如果曲面在某点没有切平面，那么在该点就没有法线 。例如，圆锥的顶点以及底面的边线处都没有法线，但是圆锥的法线是几乎处处存在的 。通常一个满足Lipschitz连续的曲面可以认为法线几乎处处存在 。
以上资料参考

• 椭圆的内法线怎么,高数
• 淀粉如何做成胶水,自制胶水简单的做法
• 滚筒洗衣机可以洗双面羊绒,如何清洗羊绒衫不缩水
• 拼多多不小心点到已收货怎么办？如何延长收货？
• 拼多多商家版如何暂停接单？怎么设置周末不收货？
• 白色车子黑色擦痕如何去掉,白色车牌是什么车
• 剑与远征如何绑定手机,《剑与远征》ios账号可以在安卓手机玩
• 法线方向怎么,法线的方程怎么
• 扔实心球要练什么,实心球如何练臂力
• 侵犯著作财产权怎么定罪,侵犯知识产权如何定罪量刑