文章图片

• 量子计算机可以解决难题 ， 比如大数的因式分解 。

在量子计算中 ， 一些基本的门构成了更复杂算法的基础 。 这些都是:
X门 ， 翻转qbit：

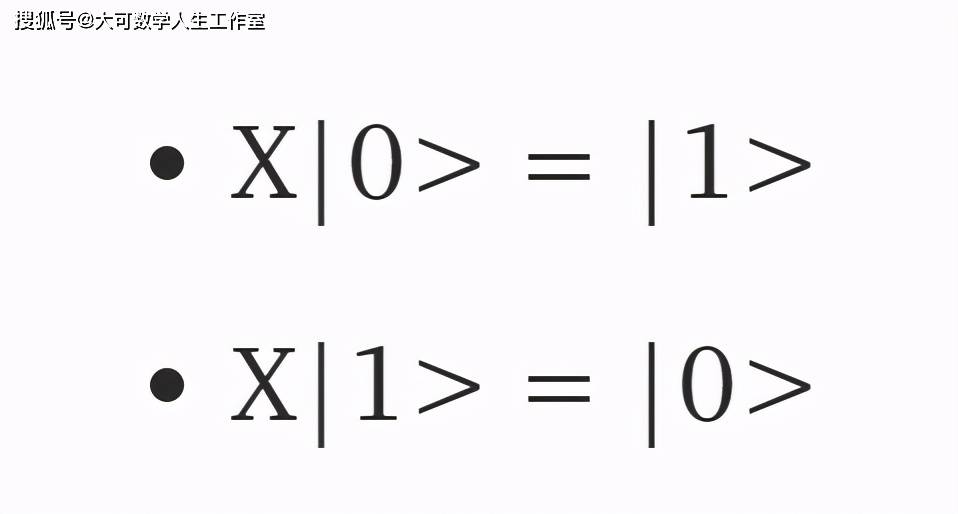
文章图片

阿达玛门 ， 在两个量子位元之间产生纠缠：

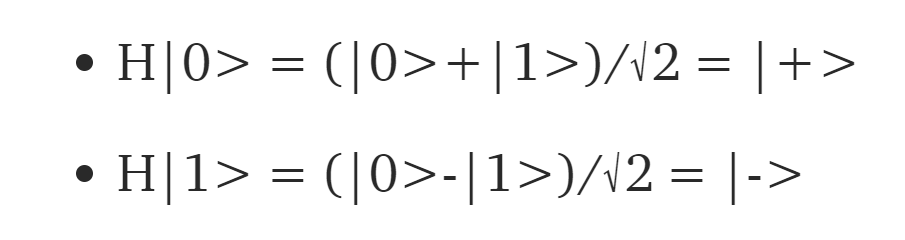
文章图片

相位门 ， 旋转波函数的相位：

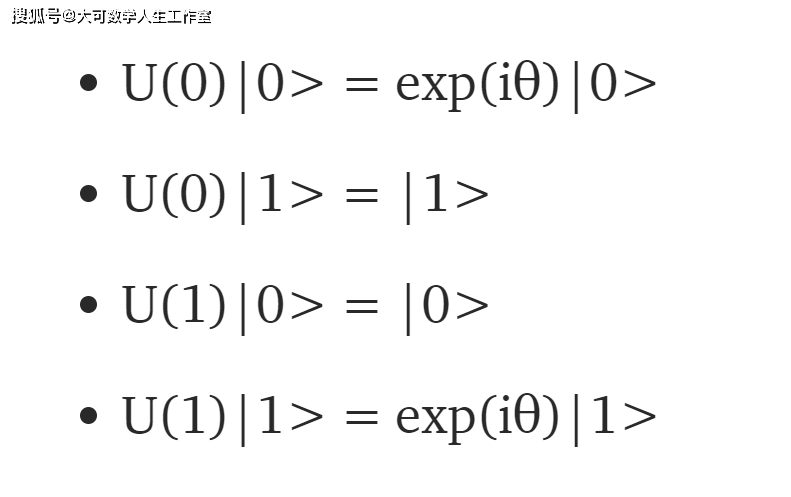
文章图片

控制非（CNOT）门：

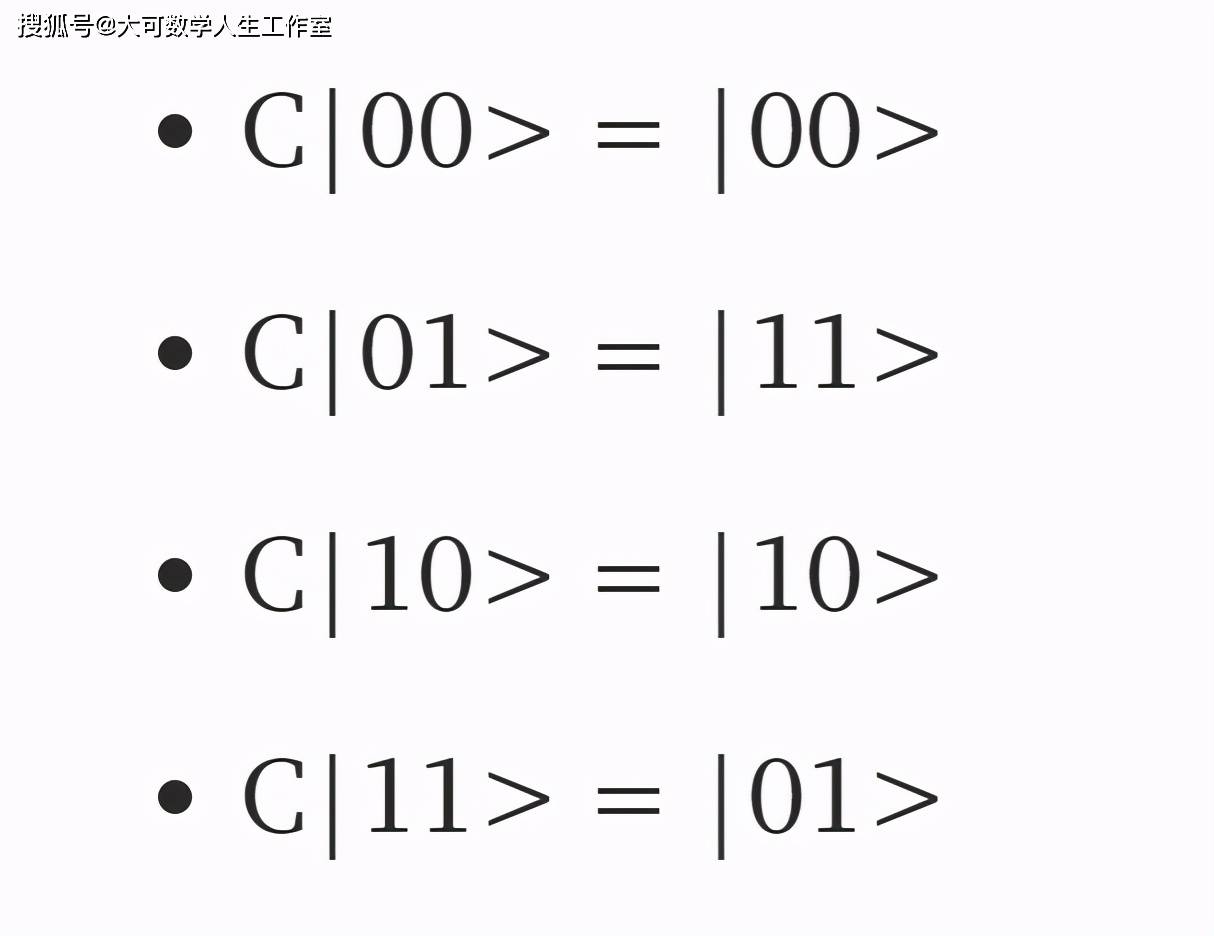
文章图片

在某些情况下 ， 涉及超过2个量子比特的算法可以被分解成更简单的二进制运算 ， 也就是上面列出的二进制运算的组合（张量网络） 。

文章图片

量子计算机 我们为什么需要量子计算机？因为它们可以解决难题（但不一定是NP难题 ， NP问题 ， 我专门写过文章介绍） 。
研究主要有两种途径 ， 一种是研究算法的发展 ， 另一种是研究能够运行这些算法的硬件的构建 。 这两个领域的发展都非常迅速 ， 创新和一些突破以指数级的速度发生 。
首先 ， 我们来谈谈硬件 。 有两类设备 ， 一类是基于量子等效退火 ， 另一类是利用其他现象来处理量子比特的状态 。
量子退火比较容易理解 。 一组原子可以设定在某一状态 ， 然后让它向能量最小的方向演化 。 想象一个有山谷和山峰 ， 我们的目标是找到最深的山谷 。 量子系统的独特之处在于隧穿 ， 也就是说 ， 系统可以在不需要克服能量障碍的情况下降到最低 。 这种方法对普遍存在的优化问题特别有效 。 问题在于 ， 只有能用伊辛模型的哈密顿函数来表述的问题 ， 目前才能在这类机器上解决 。 事实上 ， 这个过程被重复了很多次 ， 所有已经找到的极小值的最小值被作为真实全局最小值的最佳猜测 ， 但如果一开始就有 ， 就不能保证总能找到 。 有些人觉得这有点作弊 ， 因为这样的机器不是通用的量子计算机 ， 不允许实现量子算法 。
另一大类量子计算机是基于噪声中等规模量子（NISQ）技术的 。 这些机器仍然不是“完全量子的” ， 但已经为用户提供了几十个量子比特 。 不幸的是 ， 由于热激励产生的噪声限制了可执行的电路数量 。 有一件事是肯定的 ， 一台100量子位元的电脑不会在一夜之间改变世界 。 至于量子比特本身 ， 它们以不同的方式实现 。
不同的公司根据可行性、可靠性、噪声容忍度、成本等方面决定采用不同的技术 。 例如 ， IBM和Rigetti使用超导环 ， 英特尔部署量子点 ， 微软决定使用拓扑量子位 。

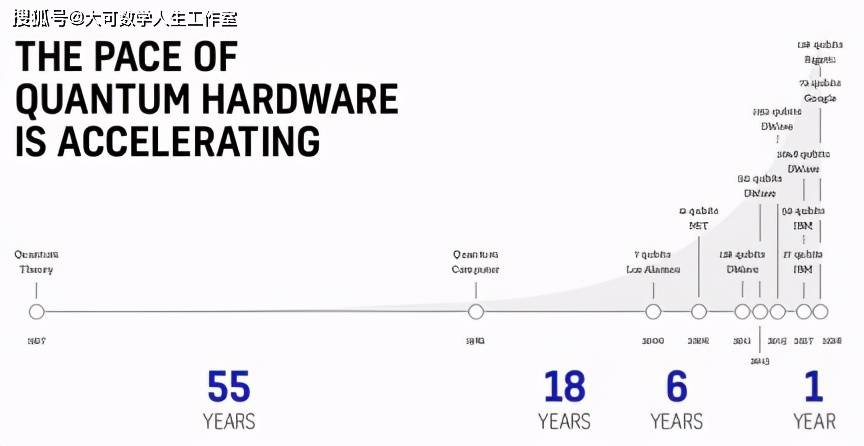
文章图片

• 量子计算呈指数级发展 。

得益于量子力学的独特特性 ， 量子计算机可以解决在经典系统上不可能或实际上不可行的问题 。
第一个令人震惊的应用是用肖尔的算法分解一个整数的因数 。 大多数常见的密码算法都是基于对一个2000位数的数字进行因式分解的实际不可能 ， 这意味着需要花上整个宇宙的年龄才能尝试所有可能的组合 ， 直到找到一个解决方案 。 另一方面 ， 量子系统的行为与传统算法不同 ， 它提供了其他途径来获得答案 ， 这是经典算法不可能做到的 ， 比如肖尔算法中使用的方法 。 任何算法的复杂性都可以用执行计算所需的操作次数来表示 。 例如 ， 扫描一个数组来查找最大值需要N次操作 ， 其中N是元素的个数 。 由所谓的戈弗算法执行的量子计算 ， 将操作次数降低到根号N ， 当N非常大时 ， 这是一个巨大的加速 。 在经典计算机上的操作需要 N^2, N^3……次 ， 但在量子计算机上需要的操作次数是NlogN ， N2logN …… 。 这个特性被称为指数加速 。