此外 , 该论文从历史演变的角度阐述了神经微分方程诞生的思路演变过程 。

文章图片
神经常微分方程
目前最常见的神经微分方程是一种神经常微分方程(neural ODE):
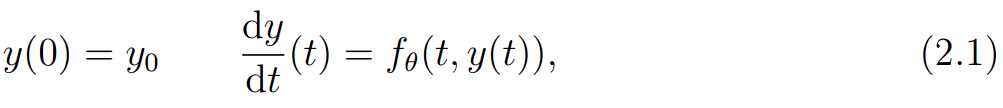
文章图片
通常这个方程需要考虑两方面的问题:(1) 方程解是否存在且唯一;(2) 评估与训练 。
与非微分方程的模型相比 , 这里存在两个额外的问题:
- 需要获得该微分方程的数值解;
- ODEnet 的反向传播 , 即通过解常微分方程直接把梯度θ求出来 。
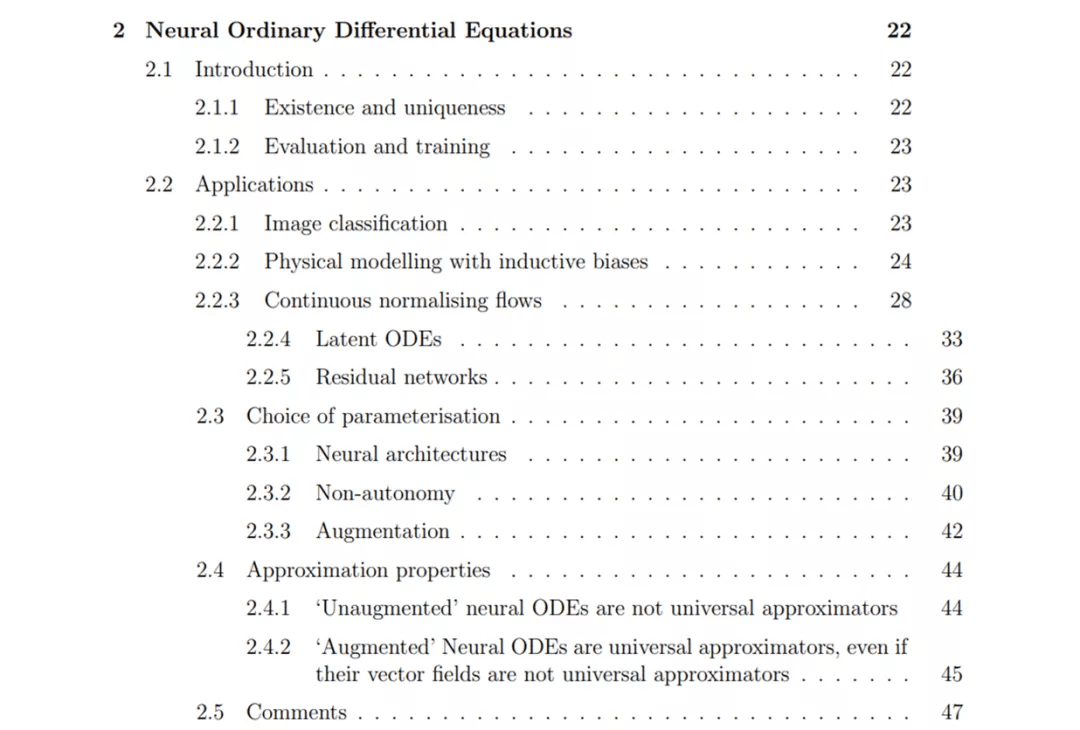
神经常微分方程的应用主要包括以下几方面:
- 图像分类;
- 带有归纳偏置的物理建模;
- 连续归一化流;
- 潜在 ODE;
- 残差网络 。
文章图片
神经受控微分方程
第三章论文从循环神经网络的连续时间限制的角度介绍了神经受控微分方程 。 这对于研究 RNN 或时间序列的人来说非常有用;也适合路径理论、控制理论或强化学习的研究者阅读 。
这一章论文首先介绍了受控微分方程(CDE)、神经矢量场、求解 CDE、正则时间序列的应用 , 然后讨论并总结了神经 CDE 的几个优点 。
论文中归纳神经 CDE 的几种应用包括:不规则时间序列、RNN 和离散神经 CDE、长时间序列和粗糙微分方程(rough differential equations)、训练神经 SDE 。
在理论属性方面 , 该论文讲解了通用近似、与 ODE 模型的比较、不变性几方面的理论 。 在参数化选择部分 , 论文介绍了神经架构与门控程序、状态 - 控制 - 矢量场相互作用两个方面 。 最后该论文从理论条件、插值点的选择、实际应用案例几方面讲解了插值方案的内容 。

文章图片
神经随机微分方程
本章共分为 6 个小节 , 主要包括随机微分方程的介绍、结构、训练标准、参数选择、示例展示以及评论 。

文章图片
随机微分方程(SDE)已广泛应用于模拟现实世界的随机现象 , 例如粒子系统 、金融市场、人口动态和遗传学。 它们是常微分方程 (ODE) 的自然扩展 , 用于对在连续时间中受不确定性影响的系统进行建模 。
SDE 的动力学由一个确定性项和一个随机项组成 , 其形式如下:

文章图片
SDE 的理论构建:SDE 是在理论基础上构建的 , 而且通常相对简单 。 一种通用且直接的方法是固定一个常数矩阵 σ , 并将σ ? d_w(t) 添加到 ODE 模型中 。
校准 SDE:一旦选择 SDE 模型后 , 必须根据实际数据校准模型参数 , 可以通过以下方式来优化:
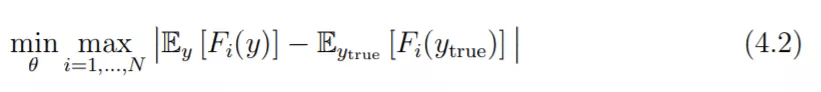
特别声明:本站内容均来自网友提供或互联网,仅供参考,请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系,我们将在24小时内删除。
