文章图片
示例展示
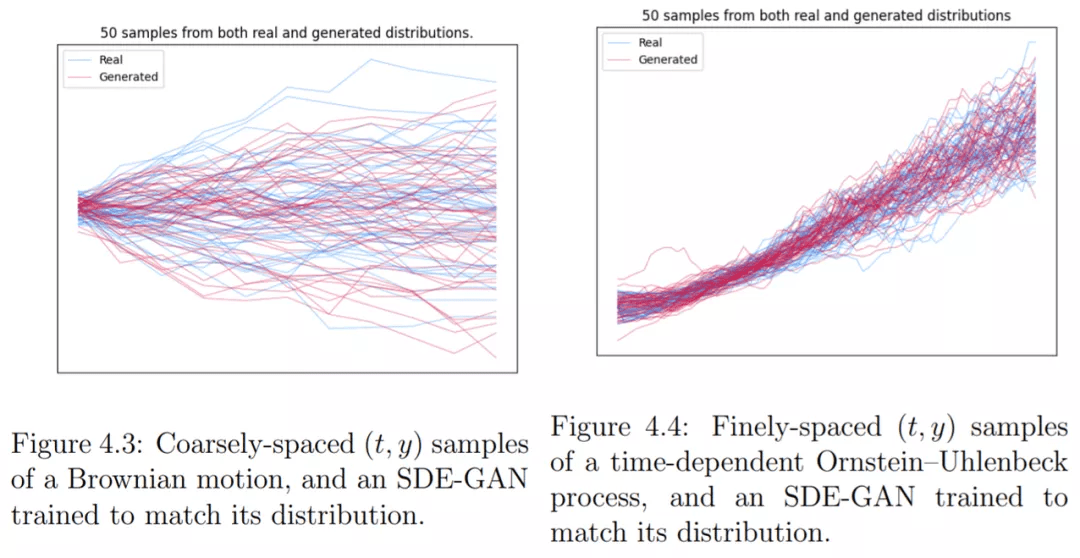
布朗运动作为最简单的示例 , 考虑(单变量)布朗运动样本的数据集 , 初始条件为 Uniform[-1, 1] 。 数据集的每个元素都是沿单个布朗样本路径的时间序列观察到的 。 研究者训练了一个小的 SDE-GAN 来匹配初始条件的分布和时间演化样本的分布 。
如图 4.3 所示 , 布朗运动可能看起来非常简单 , 但它突出了一类时间序列 , 这几乎是不可能用潜在 ODE 进行学习的(第 2.2.4 节) 。 布朗运动代表纯扩散 , 而潜在 ODE 代表纯漂移 。
文章图片
神经微分方程的数值解
本章共分为 7 个小节 , 主要内容包括通过 ODES 进行反向传播、通过 CDE 和 SDE 进行反向传播、数值求解器、实用技巧、布朗运动的数值模拟、应用软件以及评论 。

文章图片

文章图片
训练神经微分方程意味着通过微分方程的解进行反向传播 , 通过 ODE 进行微分的方法有三种:离散后优化 – 此类方法内存效率低 , 但准确且快速;先优化再离散 – 此类方法内存效率高 , 但速度有点慢;可逆 ODE 求解器 – 此类方法内存高效且准确 , 但速度稍慢 。 一般来说 , 先离散再优化是首选方法 。 但是从内存限制来讲 , 可逆 ODE 求解器是最佳选择 , 如果前两者都不合适 , 那么就采用先优化后离散的方法 , 但这类方法通常是最不受欢迎的 。
接下来文章介绍了更普遍的通过 CDE 和 SDE 进行反向传播 。
先离散后优化:这与 ODE 示例完全相同——只需通过受控 / 随机微分方程求解器的内部操作进行微分 , 通常使用在自微分框架中编写的求解器 。
CDE 的先优化后离散:这类方法有两种 , 可以为 CDE 构建连续伴随(continuous adjoint)方法 。 一种是将 CDE 简化为第 3 章中的 ODE , 然后对 ODE 应用连续伴随方法 。 还有一种是构建一个时间倒退(backwards-in-time)的 CDE , 然后通过简化为 ODE 或其他方式 , 以任何需要的方式进行数值求解 。
可逆微分方程求解器:如第 3 章所述 , CDE 可以简化为 ODE , 并且相应地可以应用于任何可逆 ODE 求解器 。 同时 SDE 有一个已知的可逆求解器 , 即可逆 Heun 方法 。
数值求解器
神经网络表示非结构化向量场 , 这意味着许多更专业的微分方程求解器(为任何特定方程开发)都不适用 , 我们必须依赖通用求解器 。
在通用求解器中 , 论文主要介绍了显式 Runge-Kutta 求解器 , 特别是 ODE 和 CDE , 它们是一个流行的数值求解器家族 , 每种求解器都需要遵循通用原则 。
除了通用求解器 , 在可逆求解器中 , 可逆求解器的反向传播如下表 1 所示 。 在可逆求解器中 , 需要局部前向来构建计算图 , 之后通过该计算图计算向量 - 雅可比积 。

文章图片
软件
用于神经微分方程的数值求解和训练的软件包目前已经进行了标准化 , 文中提供了几种选择供读者使用:
在 JAX 生态系统 [Bra+18] 的 Diffrax(第一个链接);在 PyTorch 生态系统 [Pas+19] 中的 torchdiffeq、torchcde 和 torchsde 系列库(2-5 链接);在 Julia [Bez+17] 生态系统中的 DifferentialEquations.jl(最后一个链接):
- https://github.com/patrick-kidger/diffrax
特别声明:本站内容均来自网友提供或互联网,仅供参考,请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系,我们将在24小时内删除。
