作者进一步限制并证明 ， 无论迭代是发散还是保持有限 —— 在随机梯度下降的迭代中评估的梯度函数的范数以概率 1 收敛到零 ， 并且符合预期；从而扩大了随机梯度下降可以应用于的函数范围 ， 同时保持对其全局行为的严格保证 。

发帖人表示：基于这些文献 ， 我们是否真的能够证明（随机）梯度下降有潜力在非凸函数上显示类似的全局收敛性质 ， 达到之前仅在凸函数上显示收敛程度？
但是我们仍然有理由相信（随机）梯度下降与凸函数相比在非凸函数上收敛更困难 。
网友：问题改成「梯度下降在什么条件下会收敛于非凸函数」更好
针对发帖者的这一问题 —— 随机梯度下降能否收敛于非凸函数？网友纷纷从自身经验进行解答 。 机器之心从中挑选出了几个获赞较多的回复 。
首先来看网友 @anonymousTestPoster 的回答 。 ta 表示 ， 假设存在一个表现良好的非凸函数 ， 可以参见 Issam Laradji 撰写的《非凸优化》文档 。
地址：https://www.cs.ubc.ca/labs/lci/mlrg/slides/non_convex_optimization.pdf
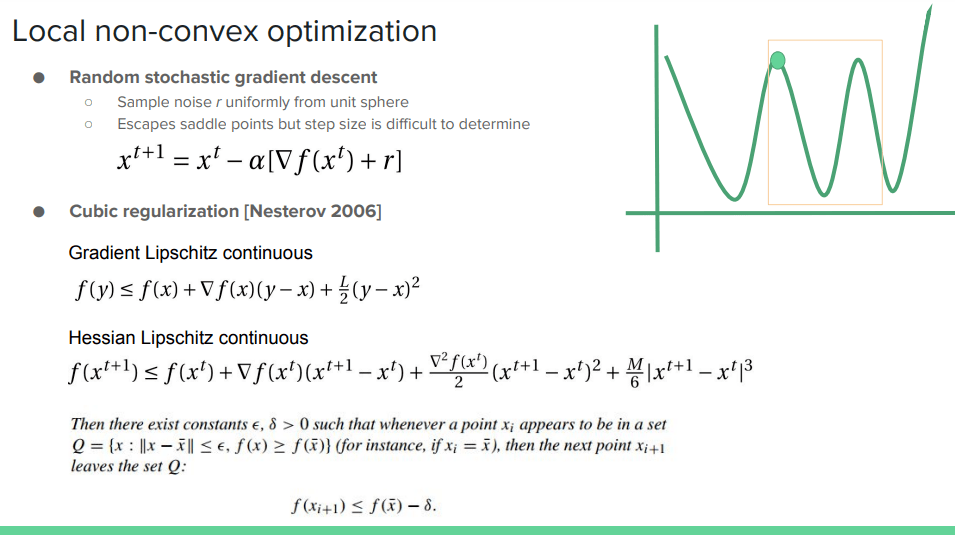
如果存在向下延伸至 Hessian 矩阵的 Lipschitz 连续性限制 ， 则文档 19 页中的 Thm 似乎表明可以不断取得进展以接近顶点 。

文章图片

如果想要更复杂的函数 ， 则几乎可以肯定需要的函数是可微的或者利普希茨连续 ， 否则只能选择一些处处连续、无处可微的疯狂函数（crazy function） ， 例如 Weierstrass 函数 。
所以 ， 关于「随机梯度下降能否收敛于非凸函数」这一问题 ， ta 认为在某些条件下「会」 ， 因为很多非凸函数它们可能扰乱 wrt 可微性 。 在提出反例时 ， 永远不要低估数学家的想象力 。
所以 ， ta 建议发帖者将问题改成「梯度下降在什么条件下会收敛于某类非凸函数」 ， 然后将每类函数作为子问题进行研究 ， 并消除打破传统梯度下降方法的非凸函数反例 。

文章图片

接着来看网友 @astone977 指出了原贴内容中存在的一些问题 。 ta 表示 ， 当发帖者认为神经网络的误差表面是非凸时 ， 则损失函数也是非凸的 。 但是 ， MSE 等损失函数是凸函数 。 将一个非凸映射（神经网络）应用于一个损失函数的输入 ， 可以创建一个非凸误差表面 。
如果我们将 MSE、BCE 等凸函数称为损失函数 ， 那么不应该使用相同的术语来描述一个神经网络的非凸误差表面 。 这在过去一直是造成混乱的根源 ， 所以 ta 指了出来 。

文章图片

最后 ， 网友 @Funktapus 也表示 ， 如果发帖者只是在讨论优化期间避免局部最小值 ， 则这是优化领域一个普遍且非常古老的问题 。 通常而言 ， 答案是「会」 。
我们可以使用随机方法来跳出小的局部最小值 。 蒙特?卡罗方法（Monte Carlo）是一种经典的方法 。 另一种方法是在开始梯度下降之前建立一个网格并找出全局最小值的大区域 。

文章图片

大家如何看待这个问题呢？感兴趣的小伙伴请在留言区积极发言 。
参考链接：https://www.reddit.com/r/MachineLearning/comments/slnvzw/d_can_stochastic_gradient_descent_converge_on/