JIT 。 JAX 允许用户使用 XLA 将自己的函数转换为即时编译（JIT）版本 。 这意味着可以通过在计算函数中添加一个简单的函数装饰器（decorator）来将计算速度提高几个数量级；

Auto-differentiation 。 JAX 将 Autograd（自动区分原生 Python 代码和 NumPy 代码）和 XLA 结合在一起 ， 它的自动微分能力在科学计算的许多领域都至关重要 。 JAX 提供了几个强大的自动微分工具；

深度学习 。 虽然 JAX 本身不是深度学习框架 ， 但它的确为深度学习提供了一个很好的基础 。 很多构建在 JAX 之上的库旨在提供深度学习功能 ， 包括 Flax、Haiku 和 Elegy 。 甚至在最近的一些 PyTorch 与 TensorFlow 文章中强调了 JAX 作为一个值得关注的「框架」 ， 并推荐其用于基于 TPU 的深度学习研究 。 JAX 对 Hessians 的高效计算也与深度学习相关 ， 因为它们使高阶优化技术更加可行；

通用可微分编程范式（General Differentiable Programming Paradigm ） 。 虽然我们可以使用 JAX 来构建和训练深度学习模型 ， 但它也为通用可微编程提供了一个框架 。 这意味着 JAX 可以通过使用基于模型的机器学习方法来解决问题 ， 从而可以利用数十年研究建立起的给定领域的先验知识 。

JAX 转换
到目前为止 ， 我们已经讨论了 XLA 以及它如何允许 JAX 在加速器上实现 NumPy；但请记住 ， 这只是 JAX 定义的一半 。 JAX 不仅为强大的科学计算提供了工具 ， 而且还为可组合的函数转换提供了工具 。
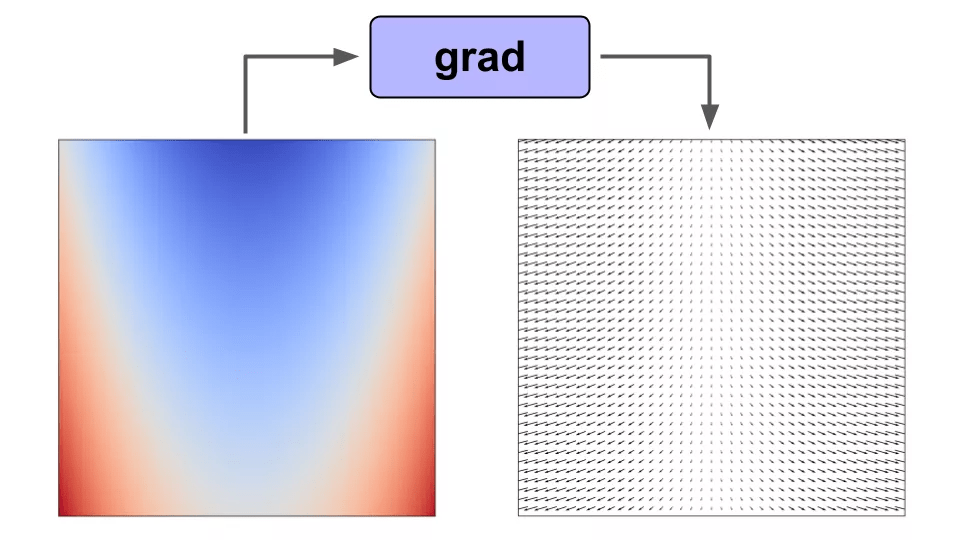
举例来说如果我们对标量值函数 f(x) 使用梯度函数转换 ， 那么我们将得到一个向量值函数 f'(x) ， 它给出了函数在 f(x) 域中任意点的梯度 。

文章图片

在函数上使用 grad() 可以让我们得到域中任意点的梯度
JAX 包含了一个可扩展系统来实现这样的函数转换 ， 有四种典型方式：

• Grad() 进行自动微分；
• Vmap() 自动向量化；
• Pmap() 并行化计算；
• Jit() 将函数转换为即时编译版本 。

使用 grad() 进行自动微分
训练机器学习模型需要反向传播 。 在 JAX 中 ， 就像在 Autograd 中一样 ， 用户可以使用 grad() 函数来计算梯度 。
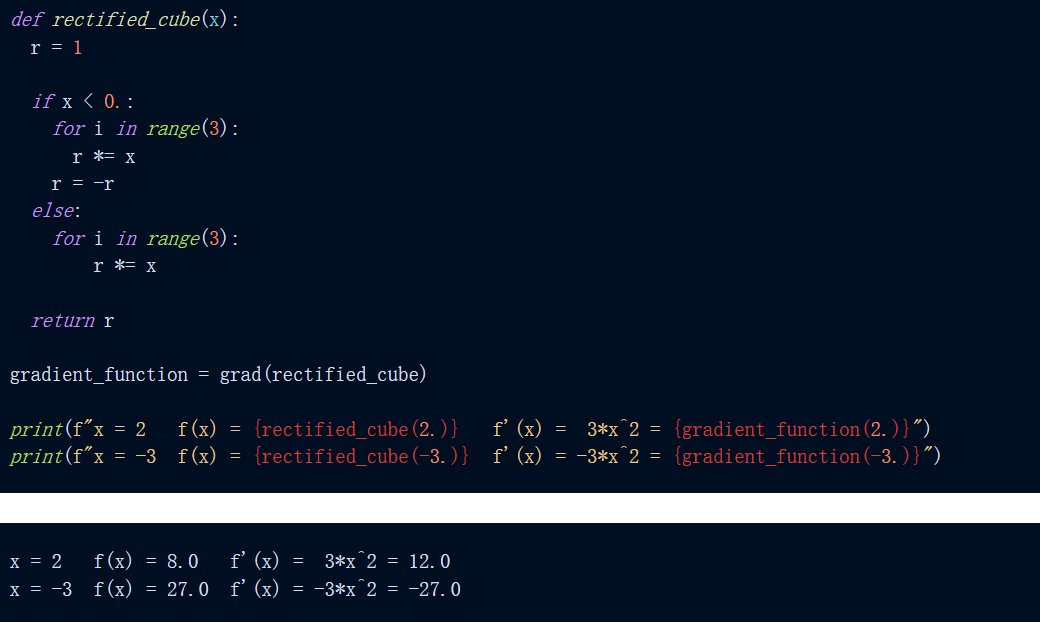
举例来说 ， 如下是对函数 f(x) = abs(x^3) 求导 。 我们可以看到 ， 当求 x=2 和 x=-3 处的函数及其导数时 ， 我们得到了预期的结果 。

文章图片

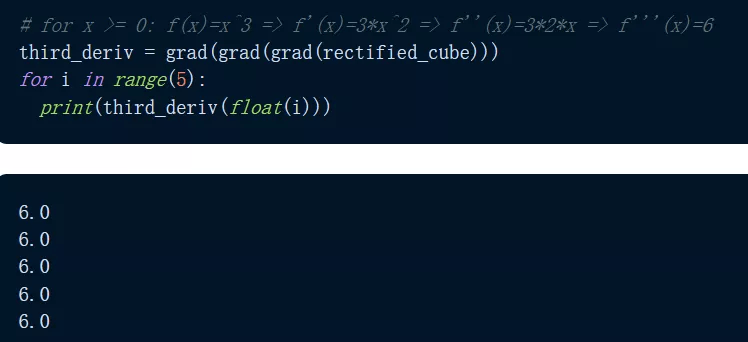
那么 grad() 能微分到什么程度？JAX 通过重复应用 grad() 使得微分变得很容易 ， 如下程序我们可以看到 ， 输出函数的三阶导数给出了 f'''(x)=6 的恒定预期输出 。
【2022年，我该用JAX吗？GitHub 1.6万星，这个年轻的工具并不完美】
文章图片

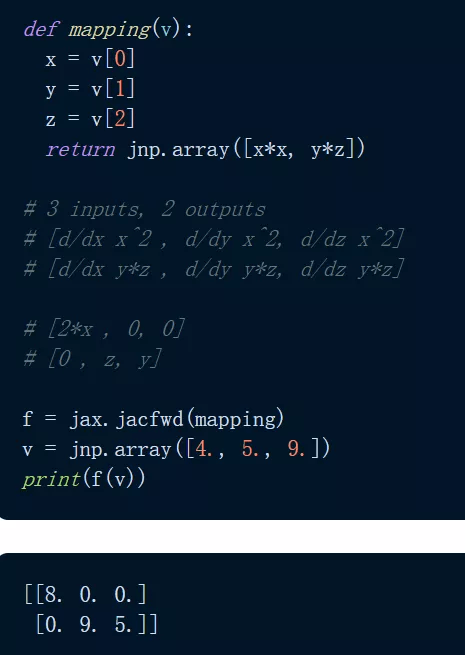
可能有人会问 ， grad() 可以用在哪些方面？标量值函数：grad() 采用标量值函数的梯度 ， 将标量 / 向量映射到标量函数 。 此外还有向量值函数：对于将向量映射到向量的向量值函数 ， 梯度的类似物是雅可比矩阵 。 使用 jacfwd() 和 jacrev() ， JAX 返回一个函数 ， 该函数在域中的某个点求值时产生雅可比矩阵 。

文章图片

从深度学习角度来看 ， JAX 使得计算 Hessians 变得非常简单和高效 。 由于 XLA ， JAX 可以比 PyTorch 更快地计算 Hessians ， 这使得实现诸如 AdaHessian 这样的高阶优化更加快速 。