AlphaGo的战胜人类的秘密是依靠 蒙特卡洛树搜索和深度神经网络 ， 无需遍历所有情况 ， 即可在有限的时间内找出最佳一着 。

文章图片

1、什么是蒙特卡洛算法？
20世纪40年代美国开启了研制原子弹的“曼哈顿计划” ， 这个计划的领导者是现代计算机之父冯诺依曼 。
在研制原子弹的过程中 ， 冯诺依曼提出了一种新的算法 ， 通过大量随机样本去了解一个高度复杂的系统 ， 并把这个算法命名为“蒙特卡洛算法” 。
蒙特卡洛是摩洛哥的一座城市 ， 以赌博出名 。 赌博还是算法 ， 都与概率和随机性有关 。 所以 ，蒙特卡洛算法的核心就是——蒙 。
2、怎样认识蒙特卡洛法？
我们可以用NetLogo设计一个蒙特卡洛法计算圆周率的程序 ， 让学习数学变得更简单 ， 也为我们提供一个新的思维方式 。

文章图片

蒙特卡洛法其实很简单 ， 如上图 ， 首先我们作圆以及圆的外界正方形 。 假设圆的半径为R ， 则外接正方形边长为2R 。
接下来 ， 我们在正方形内随机投点如果随机投点 。

文章图片

假设我们总共投进了a个点 ， 落入圆内的点有b个 ， 那么 ， a和b的比例是多少呢？
根据面积公式可求 ， S圆=πR2 ， S方=4R2 ， 我们很容易得知 ， b/a ≈ S圆/S方 = πR2/4R2=π/4 。
这样我们就建立起一个落在圆内的概率（b/a）和圆周率π的关系 ， 通过简单的移项 ， 我们获得了π与投点个数的关系： π ≈ b/a×4 ， 这样我们就可以通过计算b和a的数据计算圆周率π 。
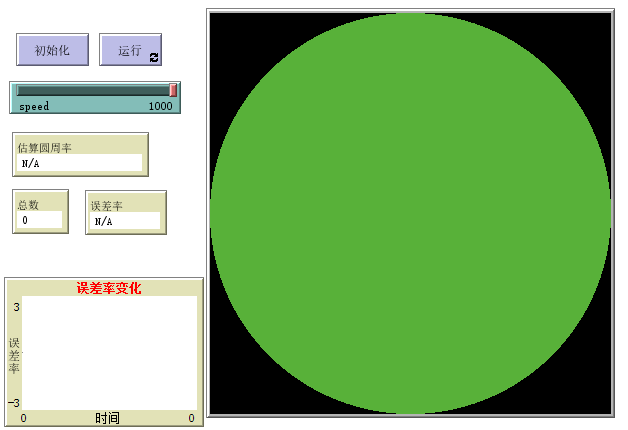
点击运行 ， 右侧的舞台上就会随机出现小海龟 ， 我们可以通过统计站在绿色区域的小海龟和总共出现的海龟比例 ， 来估算圆周率 。 点击运行 ， 我们可以看到无填上出现了很多小海龟 。

文章图片

通过下方误差率表统计着估算的圆周率与高精度的圆周率之间的误差率变化 ， 我们看到 ， 一开始是误差率非常高 ， 随着投点数量的增加 ， 误差率慢慢接近于0.也就是说 ， 只要我们进行足够多的投点 ， 就可以获得精度较高的圆周率 。

文章图片

3、如何用NetLogo设计蒙特卡洛法计算圆周率的程序？
我们用下面两个流程图展现初始化与运行两个按钮的程序 。

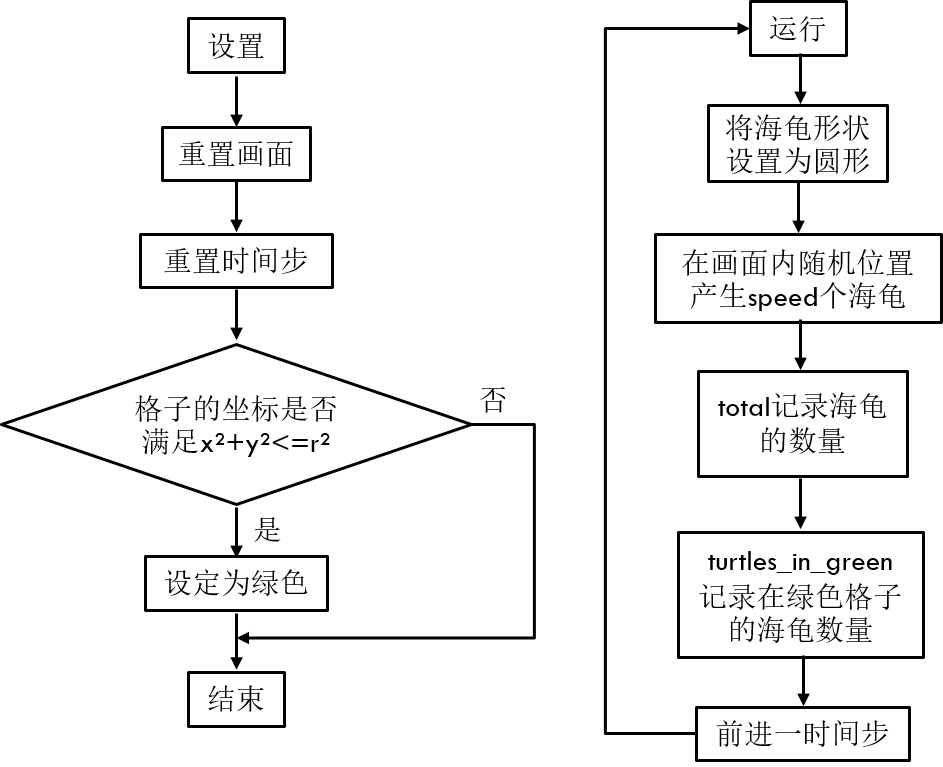
文章图片

而计算圆周率的程序可以通过监视器完成 ， 程序只有一句话：
( turtles_in_green / total ) * 4
这就是我们之前说的 π ≈ b/a×4 。
4、蒙特卡洛法有哪些特点？
我们来总结一下 。
首先 ， 蒙特卡洛法需要进行多次重复试验 ， 多次投点才能获知圆周率；蒙特卡洛法的精确度低 ， 数万次乃至数十万次投点 ， 才将圆周率误差提高到0.01% 。

文章图片

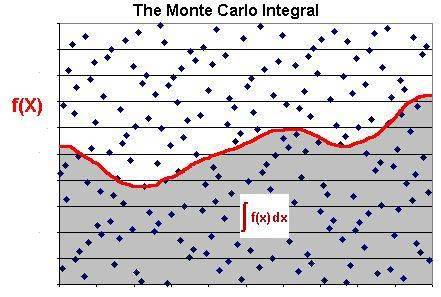
从另一方面看 ， 蒙特卡洛法有较高的泛用性 ， 许多很多可以使用积分求面积的计算也可以通过蒙特卡洛法得到 ， 对于不规则图形甚至可能是唯一方法 。
蒙特卡洛法还有计算简便的特点 ， 对于复杂度极其高的计算 ， 蒙特卡罗法更为简便 。