文章图片	可能没有一个数字像π那样神秘、浪漫、被误解或激发人们的兴趣 。 ——威廉·舒哈夫 《π的自然与历史》

【走近神秘的数字π！手把手教你用蒙特卡洛法来计算圆周率】数学可以说是无处不在 。从自然模式到气候科学 ， 从医学成像到搜索引擎 ， 从运输网络到AI的优化 ， 从建模到流行病的控制……数学在我们日常生活的几乎每个领域都发挥着至关重要的作用：
联合国教科文组织在2019年11月26日第四十届大会批准宣布 ， 3月14日为“国际数学日（International Day of Mathematics,简称IDM）” 。 因为“3.14”是圆周率数值最接近的数字 ， 所以这一天也叫圆周率日（π Day ） 。
圆周率π是一个迷人的数字 ， 人们对它的认识推动了数学的长足进步
圆周率 ， 一般以π来表示 ， 是一个在数学及物理学中普遍存在的数学常数 ， 它是圆形的周长与直径的比值 。 研究π的历史可以追溯到几千年前 ， 它是数学家们一直以来追踪的目标之一 。
公元前250年 ， 希腊数学家阿基米德通过 割圆术计算圆周率 ， 阿基米德进行了96边形的割圆之后 ， 将圆周率推到了小数点后两位3.14 。

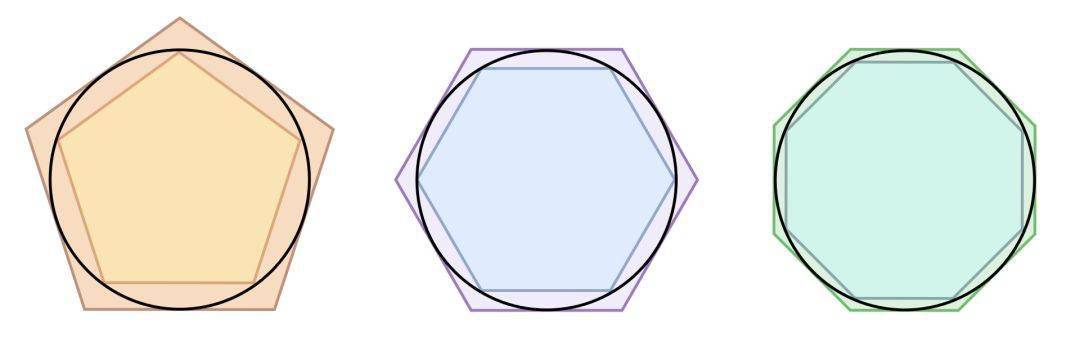
文章图片

直到公元265年 ， 中国的数学家刘徽用割圆术的方法 ， 通过正3072边形计算出π的数值为3.1416 ， 艰难地把圆周率推到了小数点后四位 。
200年后 ， 祖冲之继续使用割圆术计算12,288形的边长 ， 将圆周率推到了小数点后六位 ， 可惜的是 ， 由于文献的失传 ， 祖冲之的计算方法我们现在已经不得而知了 。
祖冲之将圆周率π的记录保持了800年 。 随着近代数学的发展 ， 数学家韦达、罗门、科伊伦、司乃耳、格林伯格通过割圆术陆续将圆周率推到了小数点后39位 ， 这个精度是什么概念呢 ， 如果我们通过小数点后39位的圆周率计算一个一个可观察宇宙大小的圆 ， 计算的误差仅仅只有一个氢原子大小 。
十六世纪到十七世纪 ， 人们发现了一种新的圆周率计算方法—— 无穷级数法 ， 让计算圆周率的工作变得更加快速 。 无穷级数是一组无穷数列的和 ， 数学家梅钦通过无穷级数将圆周率推算到小数点后100位 ， 在很短的时间里 ， 人们通过梅钦类公式反复打破了新的圆周率记录 。
18世纪 ， 法国数学家布丰 提出了随机投针法 ， 即利用概率统计的方法来计算圆周率π的值 ， 也就是著名的 投针实验 。 布丰在地板上画出若干平行的直线 ， 再将一根根短于平行直线距离的针撒到地板上 ， 通过统计针的总数和与直线相交的针的个数 ， 从而计算圆周率 。

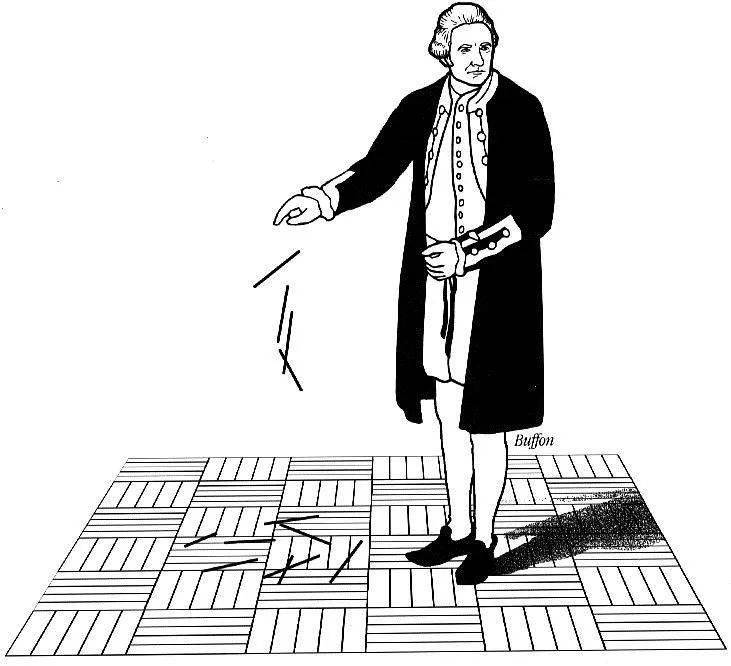
文章图片

这种算法虽然虽然没有打破圆周率的记录 ， 但这种将几何与概率结合起来的思想催生了蒙特卡洛算法 ， 也让人工智能成为了可能 。
用蒙特卡洛法计算圆周率
2016年 ， 围棋AI AlphaGo击败了顶尖的人类棋手李世石 ， 一时轰动世界 。

文章图片

围棋有19×19总共361个交叉点 ， 每个交叉点可以有黑棋、白棋、没有棋子三种情况 ， 除去围棋规则不允许和对称的情况外 ， 总共约为2x10170种情况 。 比整个宇宙的原子还多 ， 穷举法无法计算所有情况 。