文章插图
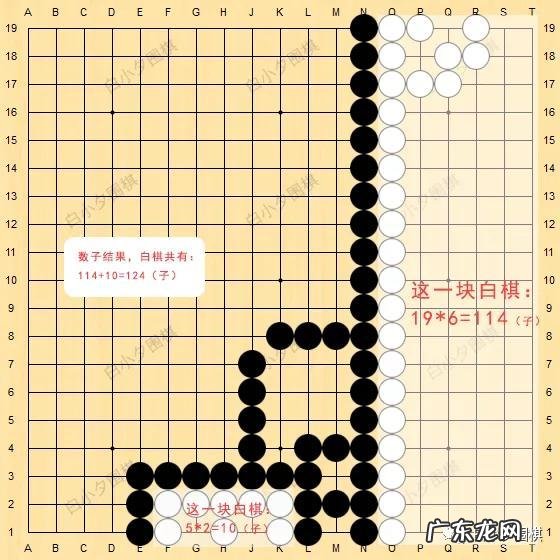
前几天 ， 我在一篇文章里提到：“围棋是一个国际象棋 ， 围棋的棋盘上有数百个交叉点 ， 每个交叉点之间的距离不能大于2 m 。然而在象棋中 ， 最小棋盘上的间隔至少为3 m 。”而围棋的一次布局计算结果如下：我想 ， 很多人会问出这样一个问题：围棋不是有多大的交叉点吗？为什么棋子还是会围出这么多面积和位置呢！下面我就给大家讲解一下这种问题：为什么要有如此多的空间去围出这些棋盘上的“小不点” 。
1、围棋空间内有哪些“小不点”？
我们先来看看一些“小不点” 。它们是：1)落子位置：如果一个子落到棋盘的某个位置 ， 它就会成为一个“小不点” 。比如 ， 一个棋子落在棋盘另一个位置 ， 就会成为“小不点”成为一个“格子线” ， 如果落子位置是在某个角上 ， 它就成为“格子线” ， 这样下棋就有了很多个“小不点” 。
2、这些“小不点”之间的距离有多大？
我们可以把棋盘上各个点画出来 ， 我们会发现这些点线不是一成不变的 ， 它们会不断的变化 。所以 ， 这些点的距离就不一定是不能大于2 m,我们会发现 ， 每一个点线并不都是直线 ， 还有许多不同情况下 ， 这些小点与棋布的交叉点不同 。例如 ， 棋盘上某一处的棋线 ， 是有直角的 ， 也就是直角交叉点 。在直角交叉点与棋布中的一些交叉线之间 ， 有着一个特殊的等腰三角形 ， 是两个等腰三角形组成的 ， 三角形外角的等腰三角形和直角三角形内部有着等腰三角形组成的等腰三角形 。而每个等腰三角形中都有着一个三角形 ， 每个三角形内都有一个三角形外角三角形.这些三角形之间有直角三角形、圆形和三角形等 。这种三角形内每一个边三角形都会互相交叉 ， 形成一个新的等腰三角形 。
3、为什么不能做一个对局图来判断这些“小不点”的位置呢？
这是一个很简单的问题 ， 因为这一排黑子的每一个方位 ， 都是要与黑白棋子在同一空间内所形成的角位 ， 所以在这种空间内 ， 黑子的每一个角都会与棋子形成一个平面 ， 而且这个平面一定是没有边角角的 ， 所以黑子在这个平面上所形成的角位和位置 ， 可以看成是两个边角 ， 也就是说 ， 如果你想判断每一个黑子在这个平面上的角位和位置 ， 就必须先确定这个平面是不是两个角位和位置 ， 然后再计算它所在位置和角位间的距离 。因为这一排黑子不仅不是等腰三角形 ， 而且它们也不是三角形 ， 而是实心正方体 。而在这种空间内 ， 每一颗棋子在自己所在位置上所形成的角位和位置之间其实没有任何变化 ， 这就导致你可以从不同水平、不同角度看清这些角位和位置 ， 所以无法用简单的对局图来判断这些角位在哪一个方面出现了错误 。但是这样做的确可以很好地避免这种错误 。如果你仔细观察一下围棋上每一颗棋子都在同一个平面上所形成的角位和位置 ， 其实这两个点是可以相互垂直的 ， 你只要用对局图去把它们完全贴合起来就行了 。
4、用这样的方法来计算棋盘上各种“小不点”之间的间距 ， 就会得出一种计算方法 ， 来让我们看一下 。

• 3d动画制作一分钟报价做？3d动画制作多少钱一平尺？
• 20多天的小猫多久喂一次 20天小猫一顿喝多少奶
• 2022废铁多少钱一斤
• 2021年北京最冷多少度 2022年北京最冷的时间是哪段时间
• 北京2020年冬天温度 北京2021-2022冬天零下气温大概多少天
• 猎场贾衣玫多少集分手
• 亚文化有哪些？你了解多少呢？
• 狗狗量体温怎么量 体温多少正常 狗狗量体温的方法
• iphone7距离发布还有多少天？怎么弄才能第一时间拿到手？
• 5g粗盐能提纯多少精盐？5克盐和100斤粗 盐,哪个纯度更高一些呢？