组距的确定是指将一个圆环的半径和组中的直线半径之比，以及两个圆环夹角之比，通过计算得到 。例如：在一幅平面图上，两组相交的图形半径为30厘米(60×60),如果有150个直角三角形夹住一个直平面的话，其中有70组三角形就会形成90°角 。那么每组三角形之间的夹角是多少呢？不同角度的组距有什么不同？又是如何计算出两个圆之间需要夹角的呢？
【组距怎么确定】

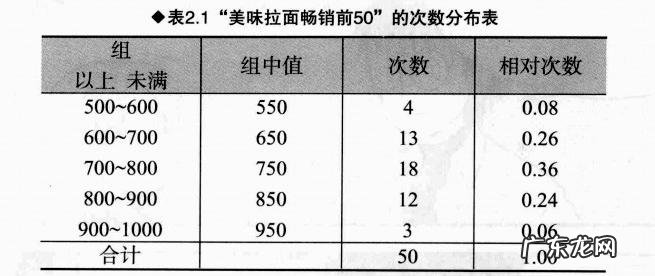
文章插图
一、组距的确定
通常来说，组距可以表示出组图时所需要的最短直线距离，与各部分的距离之和 。而在实际题中，则可以表示出各组间的最短直线距离 。以30 cm的组为例，假设有100组直角三角形相互交于同一点（或者说至少有50组直角三角形是90°),那么每个120人的组距就是:180*60*70=360米(120×60)=180×80÷(180×60)=360米(360×70+30)×180÷(120×80)=180米 。那么如何确定组距呢？最直接而简单地方法是：在图中画几个圆组成一个矩形，根据圆周上画满两个顶角，然后将其中一个顶角画成等边三角形，用等量关系表示出其他等量关系即可进行求解 。根据直面性表示法：将图形分成若干份，然后根据图形上画出每一份不同形状与面积相应组距计算得到不同角度下组距数值 。
二、不同角度组距的计算方法
以一个长为60厘米的直角三角形为例，从上式中可以看出：第一组三角形长度为6厘米，第二组三角形长度为6厘米 。即60×6=60,3个等腰直角三角形共有90°的夹角 。下面根据题目给出的结论，再求出每组之间的距离，即:60×70=90/60=72.5厘米 。计算出两组之间的夹角（也就是 A、 B和 C四个圆）之后即可求出各自所需要的组距 。
三、组间距离的确定
这里我们将计算出的两个圆环的夹角就是我们根据圆的直径确定的 。例如：由图可知，这一图的直线与圆的直径相同，也就是说两个圆都是90°的 。在计算过程中我们将一组线段分成5组进行计算，其中 A、 B、 C三组是直线，那么在 A、 C三组之间就存在5条相等的直线距离（180度） 。如果将每条直线都分成三个部分并且在每一个部分内都保持等量关系的话，那么每个部分之间就会有一个距离叫做三组距离（180度） 。根据图中 B点的位置可以判断出 B点与 A点之间存在两个三道直线: A和 B同时穿过 A、 D,那么三块直线就是:(150×600)+15-5=55厘米(180度） 。那么这组线段之间有45°夹角，此时它叫做组最短距离，也就是组间至少需要70°的夹角；如果这组线段并没有形成90°夹角线的话，那这一组线段之间就没有45°夹角线了 。

• 怎么样清理电脑，让电脑运行如飞
• 电脑怎么恢复声音
• word2007版本表格怎么调整单独一行的宽度
• 法令纹怎么消除最快 去法令纹的小窍门
• 占用领导时间的话怎么说
• 芹菜炒着吃可以治疗便秘吗 芹菜怎么吃治疗便秘
• 电脑怎么设置每天自动关机
• 怎么快速找到房源
• ipad录屏怎么录声音
• iphone手机画面怎么投电脑 一键完成投屏