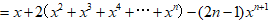
文章插图

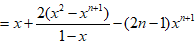
文章插图
于是

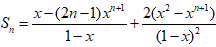
文章插图
四、用化差相减法适用于分式形式的通项公式，基本原理是把一项拆成两个或多个的差的形式，即

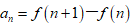
文章插图
，然后累加时中间的许多项可以抵消 。裂项凑错位相加特征，注意前后式子相等，如果不相等就要乘以一个系数 。
常用公式：

文章插图
，

文章插图
，

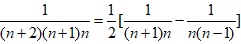
文章插图
，

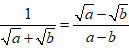
文章插图
（a≠0），

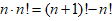
文章插图
例5、求数列

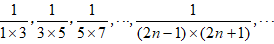
文章插图
的前n求和 。解：

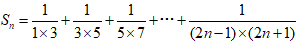
文章插图


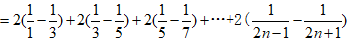
文章插图


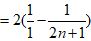
文章插图


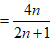
文章插图
例6、求数列

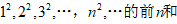
文章插图
。解：∵

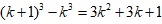
文章插图
∴

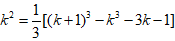
文章插图
基本原理点拨：代数式变形凑相消特征：

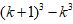
文章插图
，由此可联想求更高次方幂的n项和 。如：

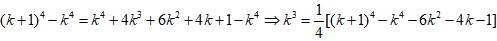
文章插图
至此，一般规律就出现了，通过变形整理便可求出

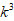
文章插图
的n项的和，以此类推，求n次方幂的问题就能彻底解决 。从而

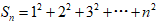
文章插图


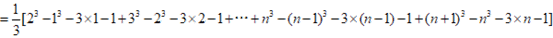
文章插图


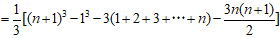
文章插图


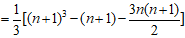
文章插图


文章插图
五、利用组合数求和公式法利用这个组合数公式，求某些特殊数列的前n和颇为方便 。因为

文章插图
，则

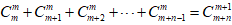
文章插图
。例7、求数列

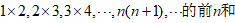
文章插图
解：∵

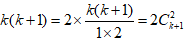
文章插图
，∴

文章插图


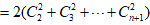
文章插图


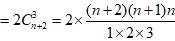
文章插图

• 为什么excel求总和会变0 求和公式excel怎么用
• excel求和不能自动填充 excel表格中一列数据怎么求和
• 转动惯量怎么求和 转动惯量计算方法
• exelce怎么排序 exelce怎么求和快捷键
• excel表格自动求和为什么会出现sum excel表中自动求和不准确
• 合并计算求和的操作步骤 word怎么求和一列数据
• 从生理需求和心理学理解祥林嫂？
• 《南京条约》对中国完成了怎样的深刻影响？仅限于割地求和吗？
• 项羽之死原文赏析 高中项羽之死课文全文翻译
• 等差数列的前n项和例题 等差数列前n项和公式