三角函数的反函数图像关于什么对称三角函数的反函数怎么求例题 _现在

小编现在给大家详细介绍关于“三角函数的反函数怎么求例题”的核心内容以及“三角函数的反函数图像关于什么对称”的相关知识，希望能够帮到您。
三角函数求反函数

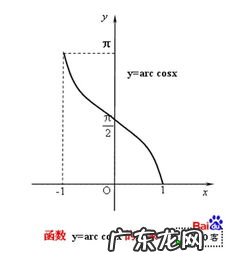
文章插图

（1）。求y=2sin3x的反函数
解：直接函数y=2sin3x的定义域应限制为：-π/2≦3x≦π/2 ，即-π/6≦x≦π/6才会有反函数。
此时直接函数的值域为：-1≦y≦1；
当-π/6≦x≦π/6时由sin3x=y/2；得3x=arcsin(y/2)；即 x=(1/3)arcsin(y/2);
交换x ， y ，即得反函数：y=(1/3)arcsin(x/2)；定义域：由-1≦x/2≦1 ，得定义域为：-2≦x≦2；
值域为：-π/6≦y≦π/6.
(2) 。求 y=sin(3x/2)的反函数
解：直接函数y=sin(3x/2)的定义域应限制为：-π/2≦3x/2≦π/2 ，即-π/3≦x≦π/3才会有反函数；
此时直接函数的值域为：-1≦y≦1；
当-π/3≦x≦π/3时有y=sin(3x/2)得3x/2=arcsiny；即x=(2/3)arcsiny；交换x ， y得反函数：
y=(2/3)arcsinx；定义域：-1≦x≦1；值域：-π/3≦y≦π/3；
三角函数为什么有反函数反函数是人为定义的，三角函数是周期函数，肯定不是一一对应，但在特定的区间（包含最大值和最小值的半个周期）是一一对应的，我们就可以定义反函数。
反三角函数是三角函数的反函数吗？是的，因为所有的三角函数，都是多个自变量对应同一个函数值，即不同的自变量可以算出相同的函数值。所以所有的三角函数都是没有反函数的。而反三角函数，是三角函数的一个单调分支的反函数，不是完整的三角函数的反函数。反三角函数是一种基本初等函数。它是反正弦arcsin x ，反余弦arccos x ，反正切arctan x ，反余切arccot x ，反正割arcsec x ，反余割arccsc x这些函数的统称，各自表示其正弦、余弦、正切、余切，正割，余割为x的角。
三角函数的反函数是个多值函数，因为它并不满足一个自变量对应一个函数值的要求，其图像与其原函数关于函数 y=x 对称。欧拉提出反三角函数的概念，并且首先使用了“arc+函数名”的形式表示反三角函数。
求证三角函数的反函数和定义域【三角函数的反函数图像关于什么对称三角函数的反函数怎么求例题】x<=0
-2x>=0
1-2x>=1
ln(1-2x)>=0
所以反函数定义域x>=0y=ln(1-2x)
e^y=1-2x
2x=1-e^y
x=(1-e^y)/2
所以反函数y=(1-e^x)/2,其中x>=0
反三角函数的反函数详细求解反函数为： y = 2sin(x/3) ，定义域为: [-3π/2 ， 3π/2]
y = 3arcsin(x/2)
y/3 = arcsin(x/2)
sin(y/3) = x/2
2sin(y/3)=x
反函数为： y = 2sin(x/3)
定义域为: [-3π/2 ， 3π/2]
扩展资料
反函数的性质：（1）函数存在反函数的充要条件是，函数的定义域与值域是一一映射；
（2）一个函数与它的反函数在相应区间上单调性一致；
（3）大部分偶函数不存在反函数（当函数y=f(x) ，定义域是{0} 且 f(x)=C （其中C是常数），则函数f(x)是偶函数且有反函数，其反函数的定义域是{C} ，值域为{0} ）。
（4）一段连续的函数的单调性在对应区间内具有一致性；
（5）严增（减）的函数一定有严格增（减）的反函数；
（6）反函数是相互的且具有唯一性。
以上内容就是关于三角函数的反函数怎么求例题和三角函数的反函数图像关于什么对称的全部内容，是由小编认真整理编辑的，如果对您有帮助请收藏转发...感谢支持！

特别声明：本站内容均来自网友提供或互联网，仅供参考，请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系，我们将在24小时内删除。

三角函数的反函数图像关于什么对称 三角函数的反函数怎么求例题

三角函数的反函数图像关于什么对称三角函数的反函数怎么求例题