文章图片

来优化 QCNN 中的参数 ， 并最小化代价函数 ， 代价函数可表示为

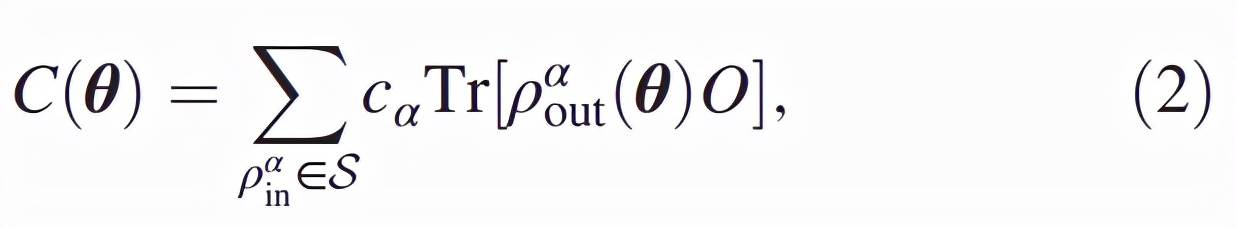
文章图片

其中 c_α是实系数 ，

文章图片

是从如下等式 (1) 中获得的 ， 每个输入状态为ρ_in 。
Ansatz
为了简单起见 ， 该研究主要考虑两种情况：n=2^k 和 L=log(n)=k ， 这样 dim(H_out)=2 。 此外 ， 该研究假设卷积层和池化层中的 unitary 是独立的 。 也就是说 ， V(θ) 中的卷积层和全连接层由作用于相邻量子比特的两个量子比特参数化 unitary 块组成 ， 表示为

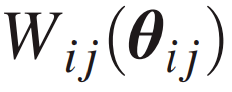
文章图片

。
研究者注意到 ， 这种泛化包含作为特殊情况的常见 QCNN 结构 ， 其中同一卷积或池化层中的块是相同的 。 此外 ， 研究者在论文的结果部分讨论得出：卷积层中的 unitary 相关性往往会增加代价函数的梯度幅值 。

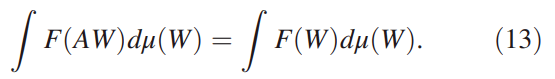
文章图片

如上等式 (13) 所示 ， 由于代价函数偏导数的方差独立于 I_ij 中的受控 unitary ， 因此可以将池化层中算子 I_ij 的作用附到卷积层中 unitary 的作用上 。 因此 ， QCNN 的张量网络表征如下图 2 所示 。

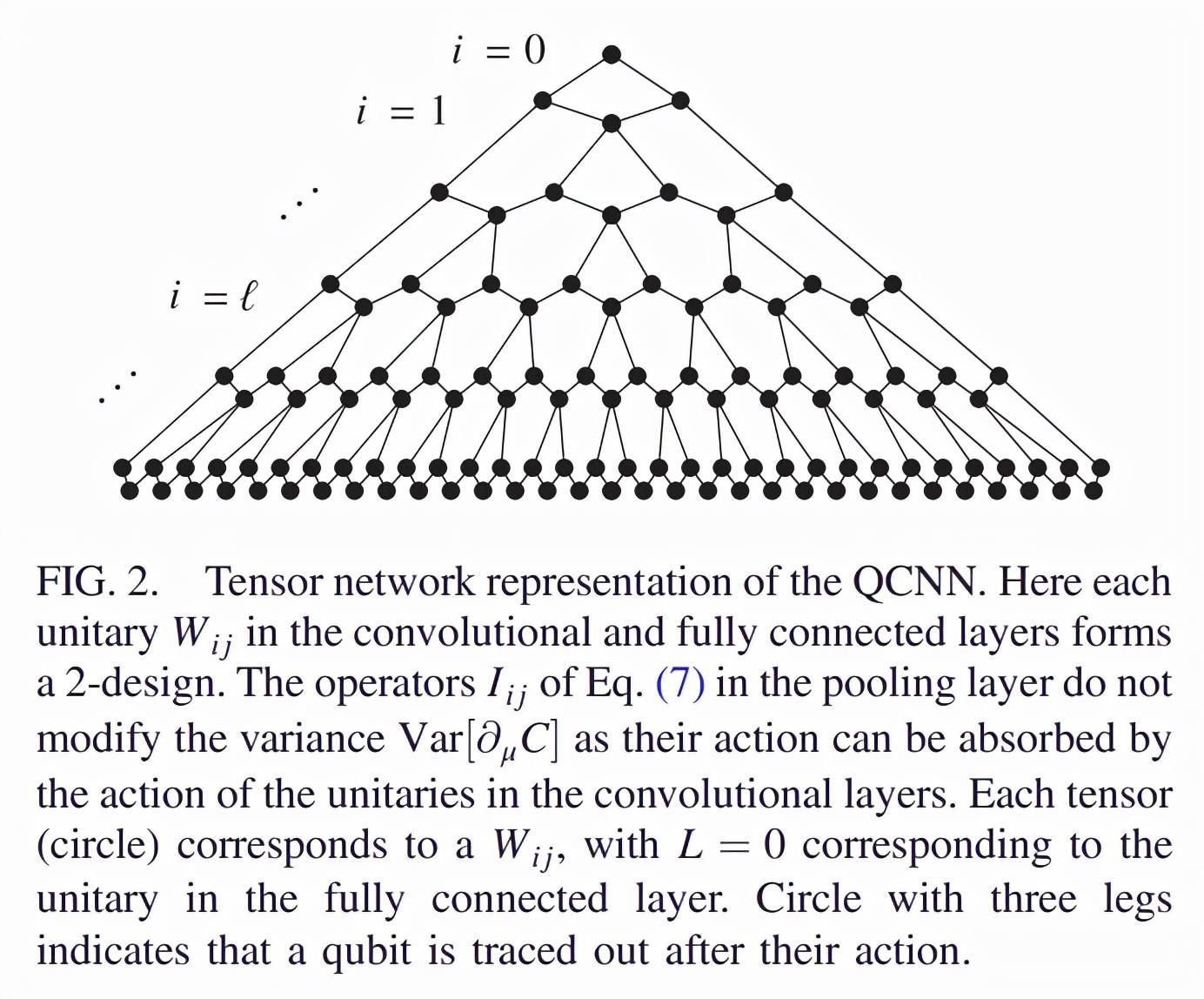
文章图片

QCNN 的张量网络表征 。
此外 ， 该研究还提出了一种分析方差缩放的新方法 ， 称为 GRIM 。

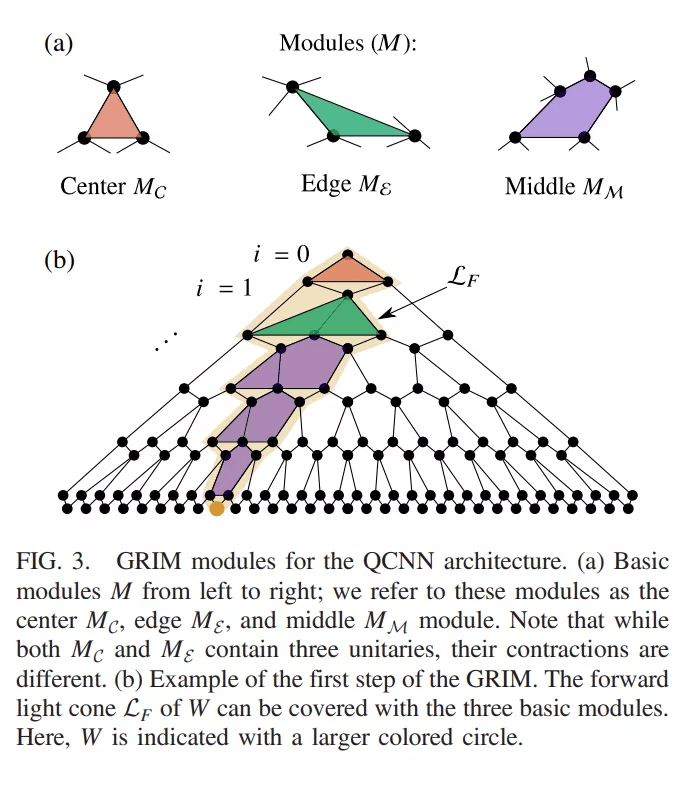
文章图片

QCNN 架构的 GRIM 模块 。
这项研究有什么意义？
作为一种人工智能方法 ， QCNN 受到视觉皮层的启发 ， 因此涉及一系列的卷积层与池化层 ， 在保持数据集重要特征的同时降低了数据的维度 。 这些神经网络可用于解决一系列问题 ， 从图像识别到材料发现 。 克服贫瘠高原是挖掘量子计算机在人工智能应用中的全部潜力并展示其优于经典计算机的关键 。
Marco Cerezo（论文合著者之一）说 ， 到目前为止 ， 量子机器学习的研究人员分析了如何减轻贫瘠高原的影响 ， 但他们缺乏完全避免它的理论基础 。 LANL 的工作展示了一些量子神经网络实际上不受贫瘠高原的影响 。
「有了这个保证 ， 研究人员现在将能够筛选关于量子系统的量子计算机数据 ， 并将这些信息用于研究材料特性或发现新材料等方面 。 」LANL 的量子物理学家 Patrick Coles 说 。
40 多年来 ， 物理学家一直认为量子计算机将被证明可用于模拟和理解粒子的量子系统 ， 这会扼杀传统的经典计算机 。 LANL 研究证明稳健的量子卷积神经网络类型有望在分析量子模拟数据方面获得应用 。
「关于激光有一句名言 ， 当它们第一次被发现时 ， 人们说它们是寻找问题的解决方案 。 现在到处都在使用激光 。 同样 ， 我们中的许多人怀疑量子数据能否变得高度可用 ， 可能意味着量子机器学习也会起飞 。 」Coles 说道 。
参考链接：
https://discover.lanl.gov/news/releases/1015-quantum-ai