经过一系列推导可得为优化下面原始目标：
2. 下面来看看拉格朗日理论：

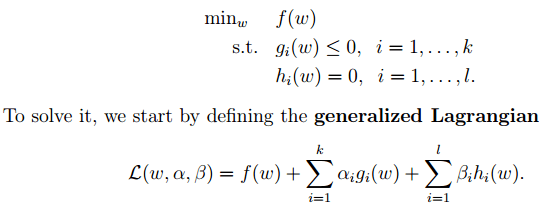
文章图片

可以将1中的优化目标转换为拉格朗日的形式（通过各种对偶优化 ， KKD条件） ， 最后目标函数为：
我们只需要最小化上述目标函数 ， 其中的α为原始优化问题中的不等式约束拉格朗日系数 。
3. 对2中最后的式子分别w和b求导可得：

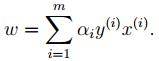
文章图片

由上面第1式子可以知道 ， 如果我们优化出了α ， 则直接可以求出w了 ， 即模型的参数搞定 。 而上面第2个式子可以作为后续优化的一个约束条件 。
4. 对2中最后一个目标函数用对偶优化理论可以转换为优化下面的目标函数：

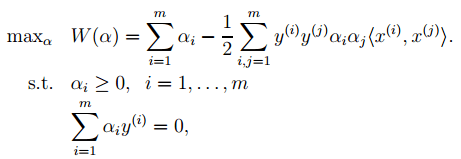
文章图片

而这个函数可以用常用的优化方法求得α ， 进而求得w和b 。
5. 按照道理 ， svm简单理论应该到此结束 。 不过还是要补充一点 ， 即在预测时有：

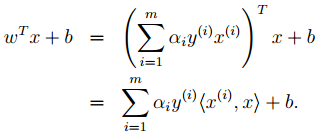
文章图片

那个尖括号我们可以用核函数代替 ， 这也是svm经常和核函数扯在一起的原因 。
6. 最后是关于松弛变量的引入 ， 因此原始的目标优化公式为：
此时对应的对偶优化公式为：

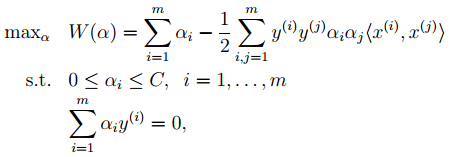
文章图片

与前面的相比只是α多了个上界 。
SVM算法优点：
1. 可用于线性/非线性分类 ， 也可以用于回归；
2. 低泛化误差；
3. 容易解释；
4. 计算复杂度较低；
缺点：
1. 对参数和核函数的选择比较敏感；
2. 原始的SVM只比较擅长处理二分类问题；
Boosting：
主要以Adaboost为例 ， 首先来看看Adaboost的流程图 ， 如下：

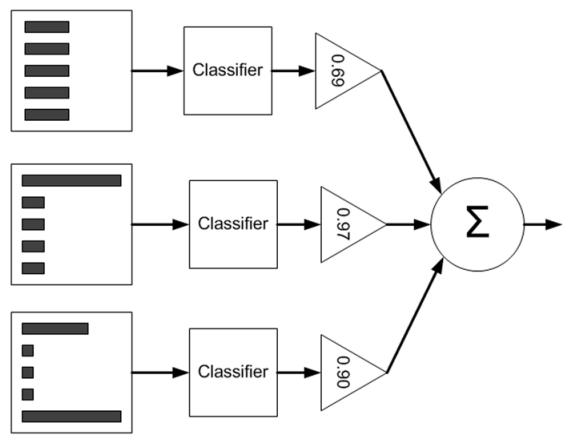
文章图片

从图中可以看到 ， 在训练过程中我们需要训练出多个弱分类器（图中为3个） ， 每个弱分类器是由不同权重的样本（图中为5个训练样本）训练得到（其中第一个弱分类器对应输入样本的权值是一样的） ， 而每个弱分类器对最终分类结果的作用也不同 ， 是通过加权平均输出的 ， 权值见上图中三角形里面的数值 。 那么这些弱分类器和其对应的权值是怎样训练出来的呢？
下面通过一个例子来简单说明 ， 假设的是5个训练样本 ， 每个训练样本的维度为2 ， 在训练第一个分类器时5个样本的权重各为0.2. 注意这里样本的权值和最终训练的弱分类器组对应的权值α是不同的 ， 样本的权重只在训练过程中用到 ， 而α在训练过程和测试过程都有用到 。
现在假设弱分类器是带一个节点的简单决策树 ， 该决策树会选择2个属性（假设只有2个属性）的一个 ， 然后计算出这个属性中的最佳值用来分类 。
Adaboost的简单版本训练过程如下：
1. 训练第一个分类器 ， 样本的权值D为相同的均值 。 通过一个弱分类器 ， 得到这5个样本（请对应书中的例子来看 ， 依旧是machine learning in action）的分类预测标签 。 与给出的样本真实标签对比 ， 就可能出现误差(即错误) 。 如果某个样本预测错误 ， 则它对应的错误值为该样本的权重 ， 如果分类正确 ， 则错误值为0. 最后累加5个样本的错误率之和 ， 记为ε 。
2. 通过ε来计算该弱分类器的权重α ， 公式如下：