图 1(b)抛出了一个尚未有答案的问题:第 r^(l-1)层从第 r^(l+1)层中中获得了什么样的层次表示 , 这些层次表示与经典的深度学习模型(如卷积网络)中获得的层次表示相比如何?图 2 示出了 [5] 中模型第一层 PE 的网络级表示 。 为简单起见 , 假定第 2 层中的表示单元 r^(2)为线性 。 在接收层 r^(2)中 , 有两个表示 16x16 大小的图像块的输入像素强度的元素 , 但只有 32 个表示元素 。 前馈连接为蓝色 W , 反馈连接为红色 W^T 。 自上而下的预测 , 表示为 I^ 。 e^(1)单元计算预测误差 。 这些想法与架构处理有关:
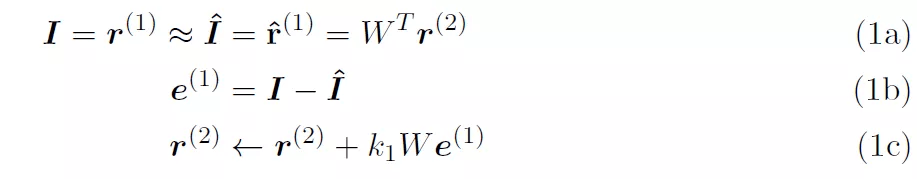
文章图片
根据公式 (1a) , I 是感官输入 , 第一层表征表示为 r^(1) , 它们是等同的 。 I 和 I^ 的维度均为 256 x1(假设为 16 x 16 的输入图像块) 。 预测输入 I^ 也是等同于 r^(1) 。 预测输入表示为 W^Tr^(2) , 其中 r^(2) 的维度为 32 x 1 , W 的维度为 32 x 256 。 最后 , 在正常工作条件下 , 输入 I 和预测输入 I^ 应大致相等 。 公式 (1b) 将第 1 层的预测误差 e^(1)定义为实际输入和预测输入之间的差异 。 公式 (1c) 用于根据预测误差更新第二层的内部表征 。 从预测误差平方和的成本函数 J 开始 。
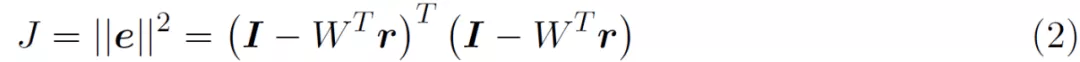
文章图片
考虑到仅针对单层网络 , 为了便于阅读 , 作者在公式中省略了层上标 。 在文献 [5] 中报告的成本函数包含了先验知识 , 但公式 (2) 的成本函数并未考虑先验知识 。 为了准备梯度下降 , 我们得到了 J 对 r 的导数 。
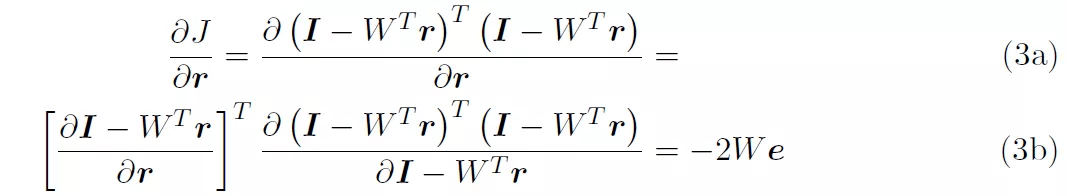
文章图片
对于梯度下降 , 我们以一定的速率沿导数的相反方向移动:

文章图片
通过取 W^T 对 J 的导数 , 可得到如下所示的学习方程:
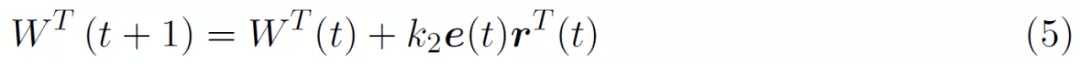
文章图片
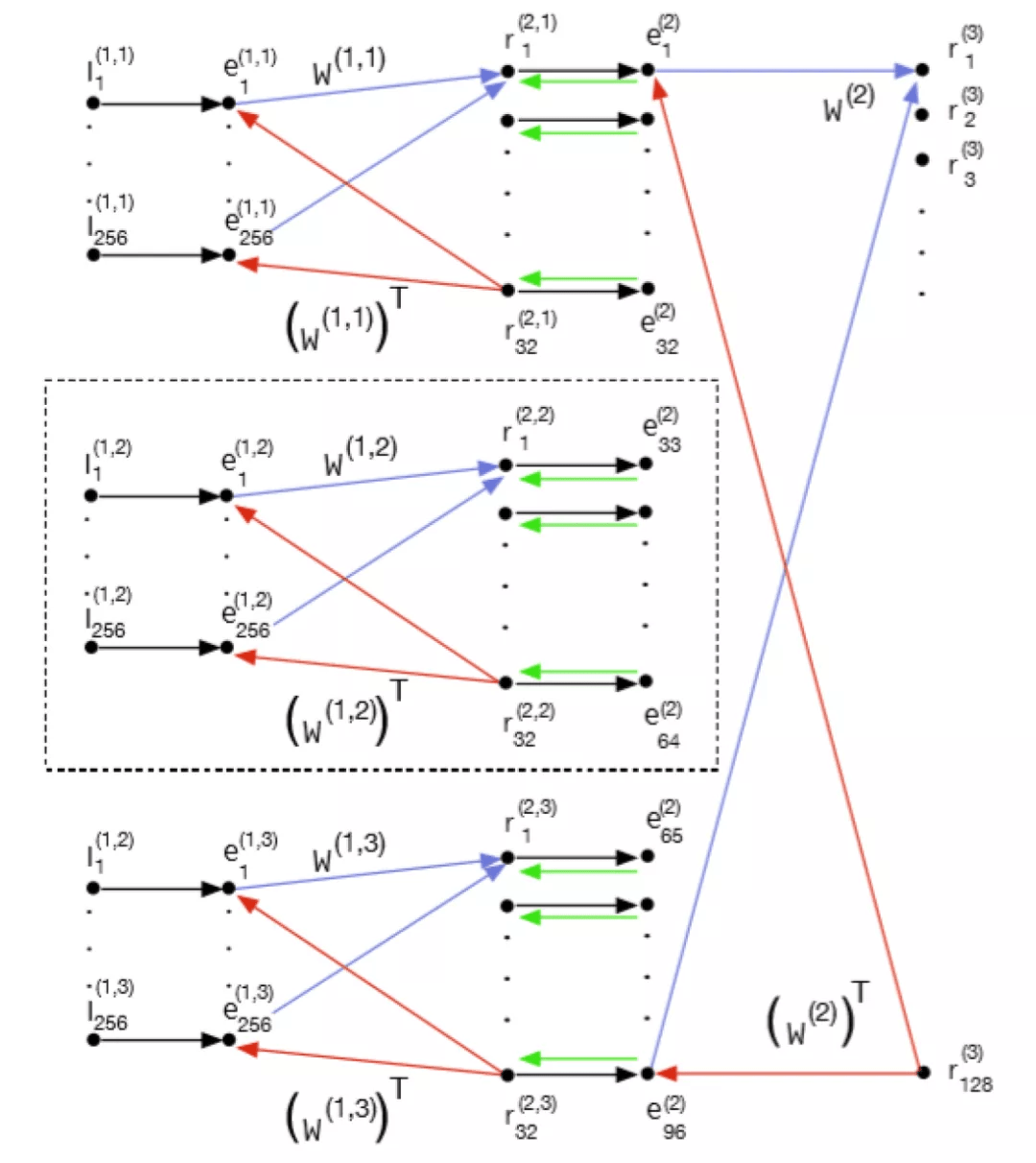
进一步的 , 给定图 2 中的模块 , 我们希望看到更大的体系结构是什么样子 , 以及当它嵌入到上下文层次结构中时会发生什么 。 为了实现这一点 , 图 3 扩展了图 2 , 在第一层中有两个横向 PE , 在第二层中增加了一个 PE 。 层 2 的输入由三个重叠的 16x16 图像块组成 。 图 2 中的神经元 (r_1)^(1)-(r_1)^(32) 与图 3 中由 (r_1)^(1,2)-(r_1)^(32,2) 识别的神经元相同 。 新添加的第 3 层接收来自第 1 层的所有 PEs 的输入 。 在图 3 中 , 第一层的中间组件对应于图 2 中的模块 。
文章图片
图 3. 扩展后的文献 [5] 中模型的全局结构 , 显示了层次结构和相邻上下文 。 图 2 中的网络位于虚线框内
3、 PredNet: 用于视频预测和无监督学习的深度预测编码网络[3]
3.1 PredNet 介绍
文献 [4] 首次提出了深度预测编码网络(deep predictive coding networks)的概念 , 而文献 [3] 中提出的模型 PredNet , 可能是使用深度学习(DL)框架实现的最早的预测编码模型 。 与上文描述的直接使用数学公式的方法相比 , 使用 DL 框架实现预测编码模型具有许多潜在优势 。
- 首先 , DL 框架非常成熟、通用且高效 。 因此 , 他们应该更容易建立和研究预测编码模型 , 唯一的复杂性是他们处理跨层反馈连接的能力 。
- 其次 , 使用 DL 框架的模型可以扩展到具有超过十万个参数的非常大的体系结构 。 这不是使用传统的预测编码能够实现的 。
特别声明:本站内容均来自网友提供或互联网,仅供参考,请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系,我们将在24小时内删除。
