文章图片

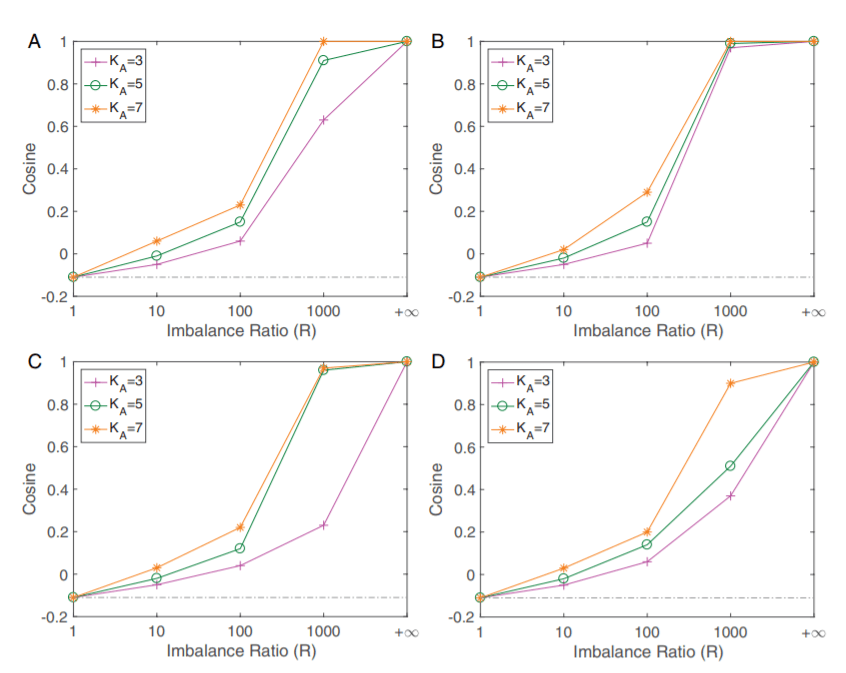
Figure 3深度神经网络中的非均衡坍缩现象 ， 横坐标R代表类之间样本数的比例 ， 纵坐标代表样本数较少的类的最后一层特征之间的方向的余弦值 。 可以看到随着R从1增加到无穷大 ， 这些样本数较少的类的特征从神经坍缩中最大化两两之间夹角的方向逐渐被挤压到相同的方向 。 ABCD四张图分别是VGG和ResNet两种网络结构在Fashion-MNIST和CIFAR10两个数据集上分别的结果 。
训练样本中的不平衡带来的公平性问题是机器学习领域长久以来的重要问题之一 ， 常用的用来缓解这一问题的方法主要是重采样 (resampling) 和重赋权 (reweighting) 两种方法 。 在文章中 ， 研究者通过层间剥离模型给出了这两种方法有效性的理论保证：文章从数学上严格证明了利用重采样和重赋权技术 ， 深层神经网络的对称性可以被完全修复 ， 神经坍缩中最大化不同类之间分类器和特征各自夹角的简单等角紧框架结构将会重新出现 ， 这就解释了为何这两种技术可以显著提升网络的泛化性能 。

文章图片

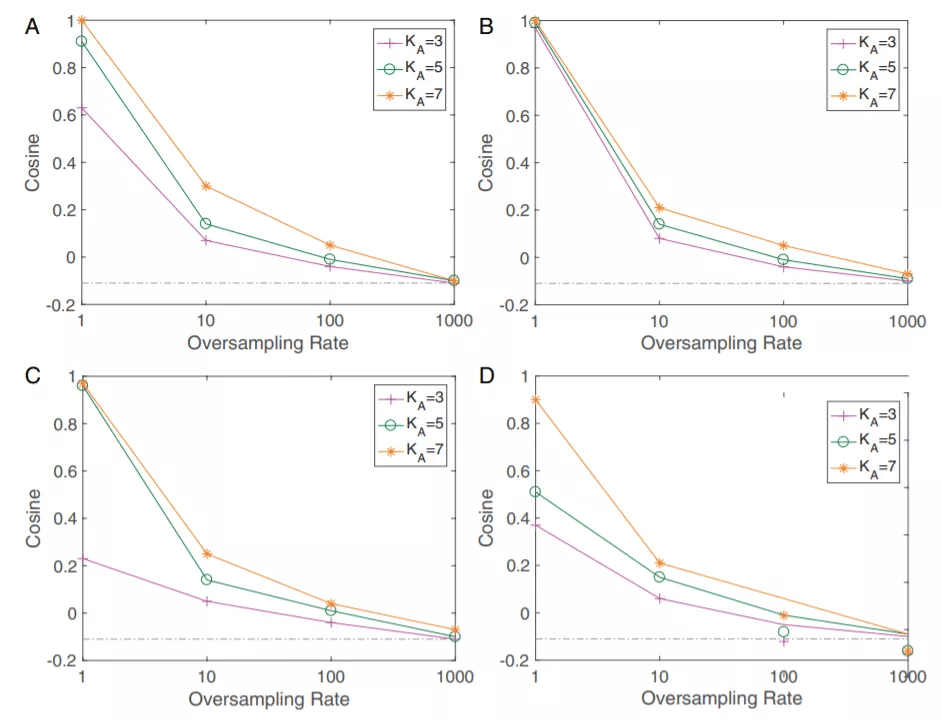
Figure 4 重采样技术对于网络最后一层对称性的修复作用 。 可以看到随着重采样比例逐渐接近类之间的样本数比例 ， 数据集不平衡造成的对称性破坏被重采样逐渐修复 ， 最终在两个比例相等时完美地重现了神经坍缩地几何结构 。 ABCD四张图分别是VGG和ResNet两种网络结构在Fashion-MNIST和CIFAR10两个数据集上分别的结果 。

文章图片

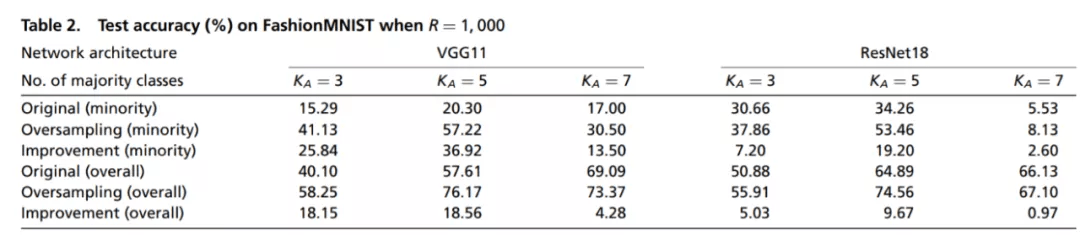
Figure 5 重采样和原始训练的泛化性能比较 。 可以看到在多种条件下 ， 重采样技术对网络泛化性能的都有显著提高 。
在后续工作中 ， 北大数院本科生冀文龙在苏炜杰教授的指导下完成的一篇文章 [3] 基于层间剥离模型对神经坍缩现象做出了进一步的理论分析 ， 文章提出了一种无约束层间剥离模型 ， 去掉了对特征和参数的约束 ， 研究了在更真实的条件下 ， 网络训练中参数的渐进行为 。 文章指出了神经坍缩现象的出现与神经网络的隐式正则化的关系 ， 并在这一非凸问题上对于网络损失函数的几何景观和梯度下降的训练过程给出了严格的刻画 ， 更精确地解释了梯度下降如何收敛到神经坍缩的几何结构 。
作为一种一般化的强有力分析手法 ， 层间剥离模型为诸多深度学习理论问题提出了一种模块化、剥离化的全新研究范式 。 进一步的研究方向包括如何利用多层层间剥离模型给出对神经网络更精确的描述？在这种情况下是否存在更强的对称性结果？如何将神经网络的训练与泛化纳入到层间剥离模型的考虑范畴内？这一模型如何为其他当下流行的深度学习理论诸如信息瓶颈 ， 隐式正则化 ， 局部弹性提供全新的视角？相信在不久的未来 ， 我们能够看到层间剥离模型带来更多令人振奋的结果 。
References
[1] Cong Fang, Hangfeng He, Qi Long, and Weijie J. Su. "Exploring deep neural networks via layer-peeled model: Minority collapse in imbalanced training." Proceedings of the National Academy of Sciences 118, no. 43 (2021).
【探秘深层神经网络对称结构，宾大提出层间剥离分析模型】[2] Vardan Papyan, X. Y. Han, and David L. Donoho. "Prevalence of neural collapse during the terminal phase of deep learning training." Proceedings of the National Academy of Sciences 117, no. 40 (2020): 24652-24663.
[3] Wenlong Ji, Yiping Lu, Yiliang Zhang, Zhun Deng, and Weijie J. Su. "An Unconstrained Layer-Peeled Perspective on Neural Collapse." arXiv preprint arXiv:2110.02796 (2021).