如果换一种场景 ， 你在选择A之后就将其打开 ， 并且看到了里面所含的金额 。在这种情况下 ， x就变成了定值 。那么在信封B中的金额只有两种可能：要么是2x ， 要么x/2；这两者的概率均为50% 。因此我们可以算出信封B中的期望金额为

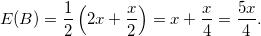
文章插图
在得知信封A中所含金额的情况下 ， 这一等式才是正确的 。它告诉我们的是 ， 就平均值来说 ， 切换信封是更优的选择 ， 悖论也不会出现 。如果在换成信封B之后 ， 你能还得到一次换回来的机会你也不会再换 ， 因为你已知了信封A里的金额少于B的期望金额 ， 因此不会再换 。
这个悖论之所以存在于文章开头所描述的版本中 ， 就是因为我们都一视同仁的看待这两个信封——即它是一种对称情况 。但是一旦你打开信封 A ， 对称性就遭到了破坏 。
值得注意的是 ， 当你打开信封A ， 并得知金额x ， 这就很可能改变你对信封B中是装有的是2x还是x/2的概率的看法 。例如 ， 如果x是一个非常大的金额 ， 那么你可能会更倾向于猜测信封B中不太可能包含双倍的金额2x 。我们将p记为信封A中含有较大数额的概率 ， 那么信封B中的期望金额E(B)则变为


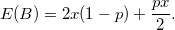
文章插图
这样我们就会发现 ， 当且仅当p < 2/3 时 ， E(B)大于 x 。换句话说 ， 只要你确信A中所含金额为较大的概率值小于2/3 ， 就应该切换信封 。
对于一部分人而言 ， 上述的方法足以解决双信封悖论 ， 但并非所有人对此都能表示同意 。在关于这一问题的思考上 ， 人们已经花费了大量的时间和笔墨了 。
译：佐佑
原文链接：
https://plus.maths.org/content/two-envelopes-problem-resolution

• 霸气潇洒的游戏昵称精选
• 照顾幼儿园宝宝的游戏 照顾宝宝的小游戏
• 征途三国版礼包 征途2经典版礼包怎么领
• 女游戏名字优雅大方 优雅好听女孩游戏名字
• 很有的游戏 一些有意思的游戏id
• 西游杀有哪些版本 西游杀网页版小游戏
• psp能直接下载游戏吗 psp怎么下载游戏?
• 弯刀迅雷下载 弯刀下 下载
• 微信小游戏荣耀之剑技能 荣誉之剑小说
• 给自己一次机会 一次机会游戏