有趣的是 ， 这种策略反映了现实生活中的很多真实情况 。
在这种策略中 ， 男士将一轮一轮地去追求他中意的女子 ， 而女子可以选择接受或拒绝相应的追求者 。 第一轮 ， 每位男士都选择向自己最心仪的女子表白 。
此时 ， 每个女子可能面对的情况有三种：没有人向她表白 ， 只有一个人向她表白 ， 有不止一个人向她表白 。
在第一种情况下 ， 这个女子什么都不用做 ， 只需继续等待； 在第二种情况下 ， 接受那个人的表白 ， 答应暂时和他做男女朋友； 在第三种情况下 ， 从所有追求者中选择自己最中意的那一位 ， 答应暂时和他做男女朋友 ， 并拒绝其他所有的追求者 。
第一轮结束后 ， 有些男士已经有女朋友了 ， 有些男士仍然单身 。 第二轮 ， 每位单身男士都从所有尚未拒绝他的女子中选出自己最中意的 ， 并向她表白 ， 无论她现在是否单身 。
和第一轮一样 ， 每位女子需要从表白者中选择自己最中意的一位 ， 拒绝其他追求者 。
注意 ， 如果这个女子已经有男朋友 ， 当遇到更好的追求者时 ， 她必须抛开现任男友 ， 投向新的追求者的怀抱 。 这样 ， 一些单身男士将会找到女友 ， 而那些已经有女友的也可能会恢复单身 。
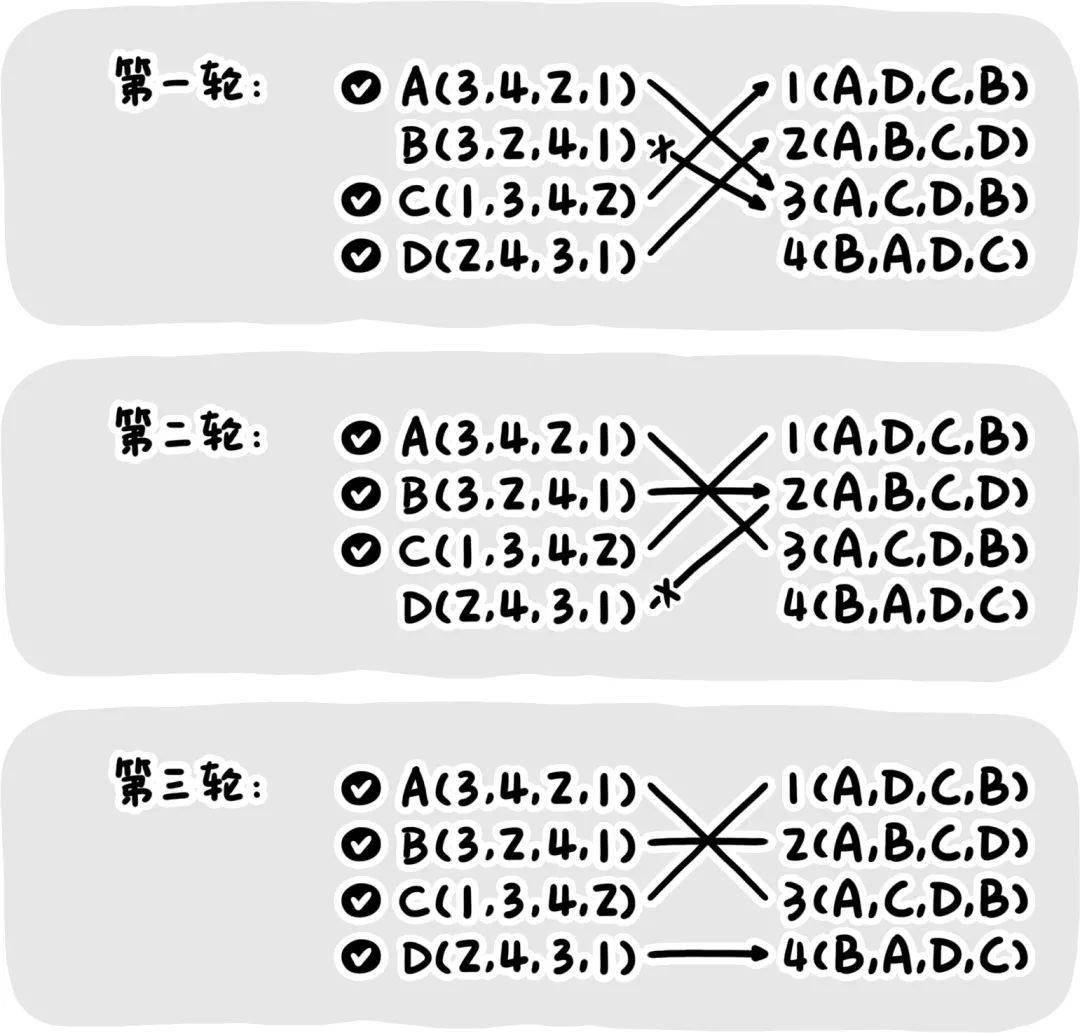
在以后的每一轮中 ， 单身的男士继续按照心目中的排序追求下一个女子 ， 而女子则从包括现男友在内的所有追求者中选择自己最中意的一个 ， 并对其他人说不 。 这样一轮一轮地进行下去 ， 直到某个时候所有人都不再单身 ， 接下来的一轮将不会发生任何表白 ， 整个过程也就自动结束 （如图 4 所示） 。 此时的婚姻搭配就一定是稳定的了 。

文章图片

图 4 应用上述策略 ， 三轮之后将得出稳定的婚姻搭配
这个策略会不会像之前的修补法一样 ， 出现永远也无法终止的情况呢？
不会 。
下面我们将说明 ， 随着轮数的增加 ， 总有一个时候所有人都能配上对 。
由于在每一轮中 ， 至少会有一个男士向某个女子告白 ， 因此总的告白次数将随着轮数的增加而增加 。 倘若整个流程一直没有因所有人都配上对而结束 ， 最终必然会出现某个男子追遍了所有女孩儿的情况 。 而一个女孩儿只要被人追过一次 ， 以后就不可能再单身了 。 既然所有女孩儿都被这个男人追过 ， 就说明所有女孩儿现在都不是单身 ， 也就是说此时所有人都配上对了 。
接下来 ， 我们还需要证明 ， 这样得出的配对方案确实是稳定的 。
首先注意到 ， 随着轮数的增加 ， 一个男人追求的对象总是越来越糟 ， 而一个女孩儿的男友只可能变得越来越好 。 假设男 A 和女 1 各自有各自的对象 ， 但比起现在的对象来 ， 男 A 更喜欢女 1 。
因此 ， 在此之前男 A 肯定已经跟女 1 表白过 。 既然女 1 最后没有跟男 A 在一起 ， 说明女 1 拒绝了男 A ， 也就是说她有了比男 A 更好的男人 。 这就证明了 ， 两个人虽然不是一对 ， 但都觉得对方比自己现在的伴侣好 ， 这样的情况绝不可能发生 。
我们把用来解决某种问题的一个策略 ， 或者说一个方案 ， 或者说一个 处理过程 ， 或者说一系列操作规则 ， 或者更贴切的 ， 一套计算方法 ， 叫作 “算法”（algorithm） 。
上面这个用来寻找稳定婚姻的策略就叫作 “盖尔–沙普利算法”（Gale-Shapley algorithm） ， 有些人也管它叫“延迟认可算法”（deferred acceptance algorithm） 。
盖尔–沙普利算法带给我们很多启发 。 作为一个为这些男女牵线的媒人 ， 你并不需要亲自使用这个算法来计算稳定匹配 ， 甚至根本不需要了解每个人的偏好 ， 而只需按照这个算法组织一个男女配对活动即可 。 你要做的仅仅是把算法流程当作游戏规则告诉大家 ， 游戏结束后会自动得到一个大家都满意的婚姻匹配 。