什么是算法？
>>>>
每当有人问我这样的问题 ， 我总会引用下面这个例子 。
假如你是一个媒人 ， 有若干名单身男子登门求助 ， 还有同样多的单身 女子也来征婚 。 如果你已经知道这些女孩儿在每个男孩儿心目中的排名 ， 以及男孩儿们在每个女孩儿心目中的排名 ， 那么你该怎样为他们牵线配对呢？
最好的配对方案当然是 ， 每个人的另一半正好都是自己的“第一选择” 。
这当然很完美 ， 但绝大多数情况下都不可能实现 。
比方说 ， 男 1 号的最爱是女 1 号 ， 而女 1 号的最爱不是男 1 号 ， 这两个人的最佳选择就不可能被同时满足 。 如果出现了好几位男士的最爱是同一个女孩儿的情况 ， 这几位男士的首选也不会同时得到满足 。
当这种最为理想的配对方案无法实现时 ，怎样的配对方案才能令人满意呢？
其实 ， 找对象不见得需要那么完美 ， 和谐才是关键 。
如果男 1 号和女 1 号各有各的对象 ， 但男 1 号觉得女 1 号比自己的现任更好 ， 女 1 号也觉得对方比自己的现任更好 ， 那么两人就可能扔下自己现在的另一半 ， 走在一起——因为这个结果对他们两人都更好一些 。
如果在一种男女配对方案中出现了这种情况 ， 我们就说这种配对方案是不稳定的 。 作为一个红娘 ， 你深深地知道 ， 介绍对象就怕婚姻关系不稳定 。 因此 ， 在给客户牵线配对时 ， 虽然不能让每个人都得到最合适的 ， 但婚姻搭配必须得是稳定的 。
现在 ， 我们的问题就是：稳定的婚姻搭配总是存在的吗？如果存在 ， 又应该怎样寻找出一个稳定的婚姻搭配？
为了便于分析 ， 下面我们做一些约定 。 我们用字母 A、B、C 对男性进行编号 ， 用数字 1、2、3 对女性进行编号 。 我们把所有男性从上到下列在左侧 ， 括号里的数字表示每个人心目中对所有女性的排名；再把所有女性列在右侧 ， 用括号里的字母表示她们对各位男性的偏好 。
图 1 所示就是有 2 男 2 女的一种情形 ， 每个男的都更喜欢女 1 号 ， 但女 1 号更喜欢男 B ， 女 2 号更喜欢男 A 。 若按 A—1、B—2 进行搭配 ， 则男 B 和女 1 都更喜欢对方一些 ， 这样的婚姻搭配显然是不稳定的 。 但若换一种搭配方案（如图 2 所 示） ， 这样的搭配就是稳定的了 。
图 1 一个不稳定的婚姻搭配（男 B 和女 1 都不满意现任伴侣）
图 2 一个稳定的婚姻搭配
可能很多人会立即想到一种寻找稳定婚姻搭配的策略：不断修补当前搭配方案 。 如果两个人互相之间都觉得对方比自己当前的伴侣更好 ， 那就让这两个人成为一对 ， 刚刚被甩的那两个人组成一对 。 如果还有想要在一起的男女对 ， 就继续按照他们的愿望对换情侣 ， 直到最终消除所有的不稳定组合 。
容易看出 ， 应用这种“修补策略”所得到的最终结果一定满足婚姻的稳定性 ， 但这种策略的问题在于 ， 它不一定有一个“最终结果” 。 按照 上述方法反复调整搭配方案 ， 最终有可能陷入一个死循环 ， 无法得出一个确定的方案（如图 3 所示） 。

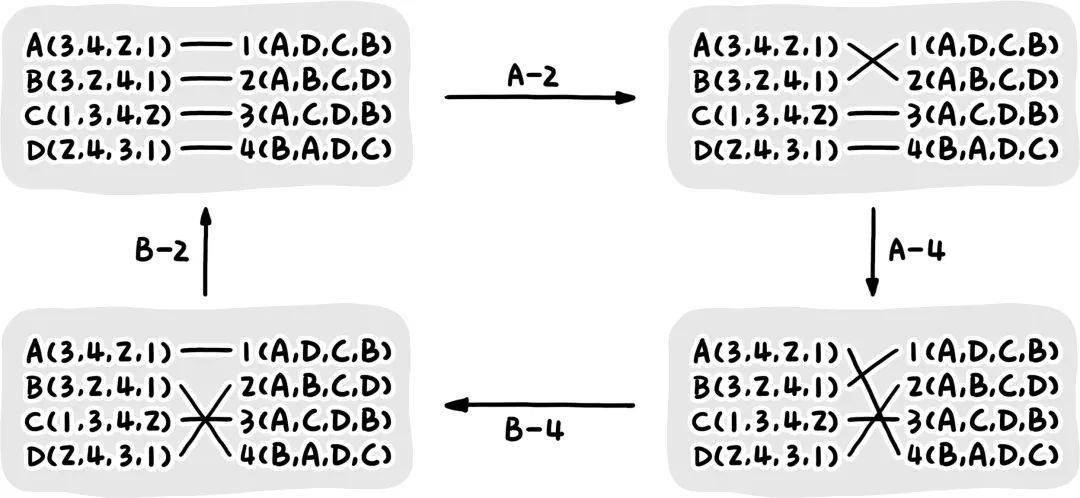
文章图片

图 3 应用“修补策略”可能会产生死循环
1962年 ， 美国数学家戴维·盖尔（David Gale）和罗伊德·沙普利（Lloyd Shapley）发明了一种寻找稳定婚姻的策略 。
不管男女各有多少人 ， 也不管他们各自的偏好如何 ， 应用这种策略后总能得到一个稳定的婚姻搭配 。 换句话说 ， 他们证明了稳定的婚姻搭配总是存在的 。