三角形三线合一可不可以证明是等腰三角形当然可以
因为三线合一的中点,所以有对线段相等
因为三线合一的角平分线,所以有对角相等
因为三线合一那条线,所以两三角形全等(HL)
不行
应该该为:
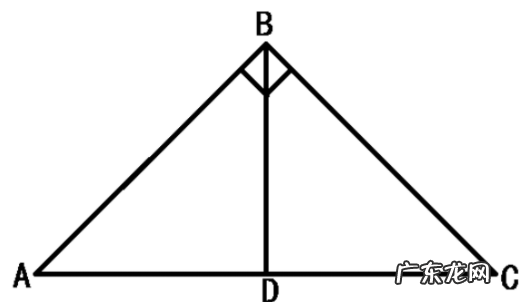
∵AD⊥BC,AD平分∠A,AD平分BC
∴AD为三角形ABC的"三线合一"
∴三角形ABC为等腰三角形
为什么三线合一不能证明等腰三角形三线合一可以证明这个三角形是等腰三角形 。相关定理如下：
1、如果一个角的角等分线与其对边的高度重合，那么这个等腰三角形就是等腰三角形 。
2、等腰三角形是等腰三角形，如果一条边的中线与另一条边的高度重合 。
3、如果三角形的角等分线与它对边的中线重合 ， 那么这个三角形就是等腰三角形 。
反之 ， 如果一个三角形是等腰三角形，则可以证明三角形三条直线的一致性 。

文章插图
注意事项：
等腰三角形三条直线的同一性证明
△ABC是等腰三角形，AB＝AC，AD是中线 。∠BAD＝∠CAD
△ABD△ACD：
BD＝DC（等腰三角形的中线将相应的边平分）
等腰三角形的性质
广告＝广告（常见的边缘）
∠坏＝∠CAD、亚行＝∠ADC
∵∵ADB＋ADC＝∠BDC（已证明） ， ∠BDC＝180°
∠亚行＝∠ADC＝90°
在BC中，有AD
等腰三角形三线合一逆定理在考试中可以直接用吗当然是可以的,因为三线 表示的是中线,顶角的角平分线,和底边上的高
这样可以证明两个三角形是全等的,则该三角形的斜边是相等的,所以两腰相等,所以等腰三角形证毕!
可以用三线合一来证等腰三角形吗可以用三线合一来证等腰三角形 。
三线合一，即在等腰三角形中顶角的角平分线 ， 底边的中线，底边的高线，三条线互相重合 。要证明等腰三角形三线合一很简单 。
可以先假设一个，然后去证明另外两个 ， 例如条件是等腰三角形和底边上的高，然后证这个高也是顶角的平分线，地边上的中线即可 ， 证明方法可以用三角形全等来证明 。

文章插图
扩展资料
定义法：在同一三角形中，有两条边相等的三角形是等腰三角形 。
判定定理：在同一三角形中，如果两个角相等，那么这两个角所对的边也相等（简称：等角对等边） 。
除了以上两种基本方法以外 ， 还有如下判定的方式：
1、在一个三角形中，如果一个角的平分线与该角对边上的中线重合 ， 那么这个三角形是等腰三角形，且该角为顶角 。
【三线合一能反推等腰,三角形三线合一可不可以证明是等腰三角形】2、在一个三角形中，如果一个角的平分线与该角对边上的高重合，那么这个三角形是等腰三角形 ， 且该角为顶角 。
3、在一个三角形中，如果一条边上的中线与该边上的高重合 ， 那么这个三角形是等腰三角形，且该边为底边 。
显然，以上三条定理是“三线合一”的逆定理 。有两条角平分线（或中线 ， 或高）相等的三角形是等腰三角形 。

• 酒精开瓶后有效期是多久,酒精有保质期 酒精能存放多久
• 受潮的花胶还能吃,花胶有点霉味还能吃
• 四季豆有斑点还能吃,四季豆有黄斑还能吃
• 菠萝是用什么才能弄熟,菠萝怎么催熟比较快 酸甜
• 木耳泡久了还能吃,木耳泡多久就不能吃了
• 三线闪光器怎么接,三线闪光器怎么接
• 酒精洗手液能带上飞机,酒精免洗洗手液可以坐飞机
• 吃百香果能吃海鲜,虾能和百香果一起吃
• 鹌鹑肉能吃吗,吃鹌鹑肉违法
• 面粉有小黑虫还能吃,面粉里有小黑虫还能吃