x+ 6 = 4
使用之前的逻辑规则 ， 没有办法得出一个真正的正解 。 由于我们的游戏中没有一个数学实体来描述这些解 ， 我们将引入一个 。 让我们称它们为负数 。 事实上 ， 只定义一个负数就足够了 ， 其他的就很容易了 。 让我们把 "负数单位 "定义为-1 ， 然后每个负数都等于其正数乘以负数单位 。
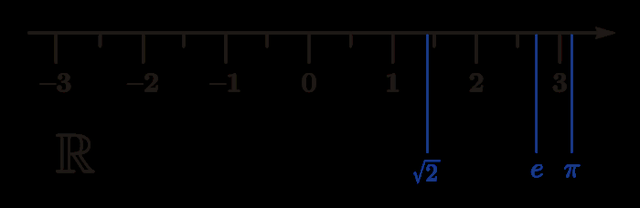
如果真实的正数在几何上可以被看作是一条从0到正无穷的射线 ， 那么负数就只是这条半线向左的延伸 ， 从0到负无穷 。

文章图片

真实线
我们可以用运算正数的方法来运算负数 。 此外 ， 我们可以利用它们的定义来摆脱我们游戏中的整个运算 ， 即减法 。 现在 ， 每当我们看到两个数字的减法时 ， 我们可以用第一个数字的加法和第二个数字的负数来代替它 。
例如 ， 5-3与5+（-3）是一样的 。
我们在很小的时候就接触到 "负数 "的概念 ， 因此我们认为这是理所当然的 ， 但如果你仔细想想 ， 它们根本不是直观的 。 在自然界中没有发现负数 。 你不能说 "那棵树上有负5个苹果" 。 负数是我们在游戏中加入的实体 ， 目的是为了进化游戏 。 然后 ， 我们为它们找到了几种解释 ， 以便在我们的现实世界中使用它们 。
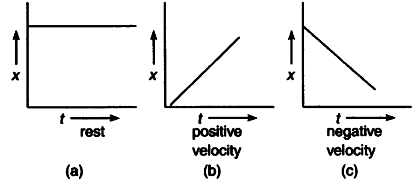
这些解释是什么？嗯 ， 这取决于 。 例如 ， 当我们谈论一个物体的速度时 ， 如果答案是一个负数 ， 那么我们就知道它的运动方向与我们最初假设的方向相反 。 在这种情况下 ， 负数被用来表示方向 。 另一个例子出现在金融领域 。 如果我们正在计算一个企业在一段时间内的总收入 ， 而我们在计算的最后发现了一个负数 ， 那么这意味着这个企业实际上正在亏损 。 在这种情况下 ， 负数表示亏损 。 对负数的解释还有很多 ， 但这两个是最突出的 。

文章图片

负的速度仅仅意味着物体在向相反的方向前进
虚数和复数
如果你已经理解了我们到目前为止所说的一切 ， 那么你已经可以预见我们将如何处理虚数的概念 。 考虑一下下面的方程 。
x^2 + 1 = 0
这一次 ， 无论是正数还是负数都无法解这个方程 。 让我们在我们的游戏中增加一些实体来玩 。 让我们定义一个新的符号i ， 是负1的平方根 。 为什么我们要这样定义一个符号呢？因为根据我们既定的游戏规则 ， 这可以解上面的方程 。 没有更深的含义 ， 就这么简单 。
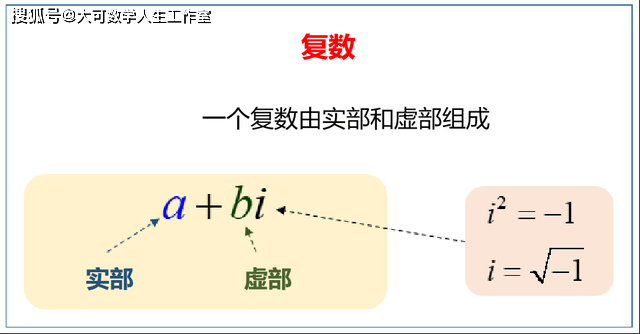
同样 ， 虚数可以使用与实数相同的代数规则进行加法和乘法 。 i+3i=4i ， i*i=-1 。 我们甚至可以将一个虚数与一个实数相加 ， 得到一个所谓的复数 。 在加法中使用的实数构成了复数的 "实部" ， 而虚数则构成了 "虚部" 。

文章图片

复数
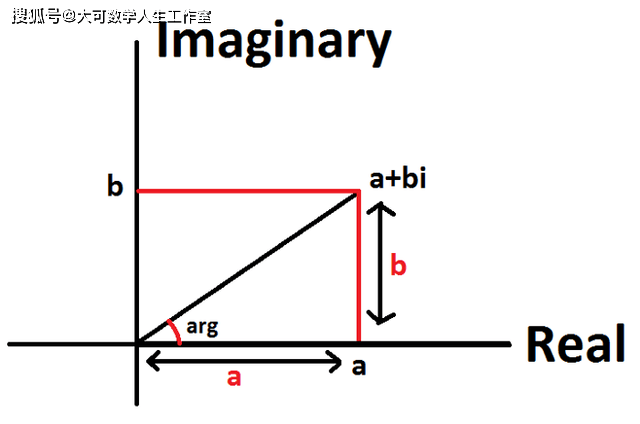
从几何学上讲 ， 就像实数一样 ， 我们可以用一条直线来形象化虚数 。 此外 ， 我们可以将虚线垂直于实线 ， 形成复数平面 ， 每个复数都对应着一个实坐标和一个虚坐标的点 。

文章图片

复数平面
好了 ， 我们已经成功地将虚数单位的概念纳入我们的游戏中 。 是时候找到一些应用和解释了 。
对于初学者来说 ， 复数在电气工程中一直被使用 。 它们是傅里叶变换的核心 ， 帮助我们分析特定信号的频率成分 。 此外 ， 在数学中 ， 包括复数在内的拉普拉斯变换帮助我们将微分方程转化为代数方程 ， 使其解更加简单 。 最后 ， 欧拉公式直接揭示了复数与余弦和正弦的联系 ， 因此 ， 当我们想描述任何类型的振荡时 ， 它们很容易被使用 。