关于虚数的一个补充说明是 ， 我们可以把一个实数与虚数单位i的乘法看作是在复数平面内逆时针旋转90度 。

文章图片

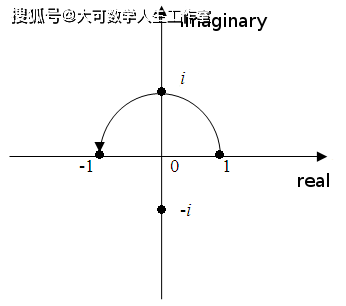
i的乘法是复数平面内的旋转
以数字1为例 ， 考虑一下 。 这个数字与正实数一起位于右侧的实线上 。 1乘以i ， 你会得到数字i ， 从1的初始点旋转90度 。 再乘以i ， 我们会得到数字-1 ， 它再次位于实线上 。 再乘以2次 ， 我们又回到了开始的地方 。
复数在现实世界中的一个应用在量子力学中很明显 。 尽管我们不会在本文中深入研究薛定谔方程（感兴趣可以看这篇文章薛定谔方程 ， 从数学上看经典力学是如何产生量子物理学方程的） ， 但事实证明 ， 只有通过复数 ， 这个我们看似随意引入的概念 ， 我们才能准确地模拟在特定位置找到一个粒子的概率 。

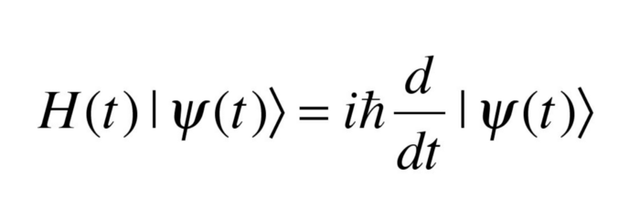
文章图片

量子力学中的薛定谔方程包含虚数单位
尽管复数在现实世界中的直接解释是有限的 ， 但其在数学中的应用是非常重要的 。 复数在许多情况下使数学变得更加容易 。 它们帮助我们描述各种现象 ， 例如以非常简洁的方式描述振荡 。 此外 ， 它们不仅使我们能够更快地解决许多问题（如微分方程） ， 而且使我们能够解决那些我们不可能只用实数对应物来解决的问题 。 虚数和 "实数 "一样真实和有用 。
在本文的最后 ， 我想回答一个你们中的许多人现在可能正在思考的问题 。 既然复数很有用 ， 为什么不发明一种新的数字？首先 ， 有 "更多种类的数" ， 叫作四元数和八元数 ， 但它们远没有复数那么被广泛使用 。 最重要的是 ， 它们是代数封闭的 。 这意味着所有复杂的多项式方程在C中都有解 ， 即复数的集合 。 没有一个多项式方程的解不是复数 。 这被称为 "代数基本定理" ， 它是由卡尔-弗里德里希-高斯证明的 。

文章图片