文章图片

老胡说科学
复数无处不在 。 从信号处理和电路分析一直到量子力学和流体力学 ， 虚数单位i似乎主导了工程和物理学中的大多数方程式 。 但这怎么可能呢？一个像i这样看似任意的数字 ， 在现实世界中没有明显的解释 ， 怎么会有如此大的作用呢？
虚数单位的符号是i ， 对于电气工程师来说是j ， 它被定义为负1的平方根 。

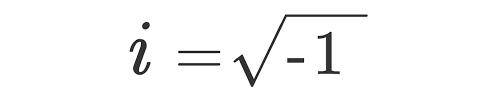
文章图片

虚数单位
但是 ， 我们在中学时都学过 ， 我们无法计算负数的平方 。 的确 ， 当第一次接触到虚数单位的概念时 ， 都会充满疑虑 。 然而 ， 为了理解它的意义 ， 我将要求你假装忘记你所知道的一切数学知识 。 我将为你提供一种看待数学科学的额外方式 ， 一种使复数不仅可取而且必要的方式 。 让我们开始吧！
数学形式主义
数学形式主义是数学哲学的主要理论之一 。
根据形式主义 ， 所有的数学都可以简化为运算公式的规则 ， 而不需要参考公式的含义 。 形式主义者认为 ， 数学符号本身 ， 而不是可能赋予它们的任何意义 ， 才是数学思想的基本对象 。

文章图片

大卫-希尔伯特
关于数学的本质 ， 这是一个非常有趣的观点 ， 首先由大卫-希尔伯特本人提出 。 根据形式主义 ， 数学可以被认为是一种游戏 。 我们有一些符号和一些规则来运算它们 。 利用这些运算规则 ， 我们得出某些句法结构和真理（被称为定理） 。 没有比这更深的意义了 。
这一切的美妙之处在于 ， 我们实际上可以利用我们人类发明的这个“游戏” ， 即数学 ， 来模拟我们在现实世界中遇到的各种现象 。 为了描述现实世界中的情况 ， 每次选择使用我们游戏中的哪些句法结构和符号 ， 往往是最困难的部分 。
到目前为止 ， 数学在描述世界方面似乎做得很好 ， 我们应该尽可能地发展它 。 如果我们以某种方式设法找到我们的符号和规则所包含的所有句法真理 ， 那么我们所要做的就是为它们中的每一个找到一个解释 ， 对吗？这正是形式主义者对数学的看法 ， 正如我们将看到的 ， 这种观点将解决在数学中发现的许多 "争议" 。
负数
在我们深入研究虚数和复数之前 ， 让我们先思考一下负数的问题 。
数学的一个关键方面是解方程 。 正如我们之前所说 ， 解方程本身并没有什么特别之处 ， 它只是一个游戏 。 然而 ， 由于在许多现实生活场景中 ， 我们对寻找某个未知量感兴趣 。 例如 ， 一个物体的速度、传递的能量、在特定位置找到一个粒子的概率等等 。 因此 ， 我们似乎有理由将这方面的游戏发展下去 。

文章图片

数学是一种游戏
谈到数字 ， 数学中引入的第一种数字是实数正数 。 我们在我们的小游戏中加入了诸如 "1 "或 "2 "或 "14.5122 "等符号 ， 因为我们看到它们有一个直观的解释 。 它们可以用来描述各种物理物体的数量 。 一个袋子里的苹果数量、一个老人的年龄和一个人的身高就是属于这一类的例子 。 这些符号是许多方程的解 ， 如以下 。
x - 20 = 5
6x - 3.1 = 4
x^3+ 4 = 5
【复数背后的直觉——从数学游戏到现实世界】然而 ， 正实数并不足以描述所有方程的解 。 考虑一下我们游戏中的符号如下：