∵DG//AB∴EF//FD
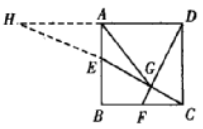
7、如图 ， 正方形ABCD中 ， E、F分别为AB、BC的中点 ， EC和DF相交于G ， 连接AG ， 求证：AG=AD 。

文章图片

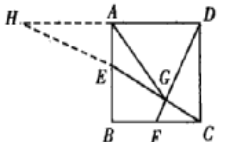
证明：作DA、CE的延长线交于H

文章图片

∵ABCD是正方形 ， E是AB的中点
∴AE=BE ， ∠AEH=∠BEC,∠BEC=∠EAH=90°
∴△AEH≌△BEC（ASA）
∴AH=BC ， AD=AH
又∵F是BC的中点
∴Rt△DFC≌Rt△CEB∴∠DFC=∠CEB
∴∠GCF＋∠GFC=∠ECB＋∠CEB=90°
∴∠CGF=90°∴∠DGH=∠CGF=90°
∴△DGH是Rt△
∵AD=AH∴AG=1/2DH=AD
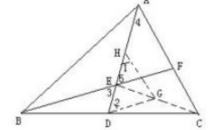
8、已知在三角形ABC中,AD是BC边上的中线,E是AD上的一点,且BE=AC,延长BE交AC与F,求证AF=EF
证明：如图

文章图片

连接EC,取EC的中点G,AE的中点H ，
连接DG,HG
则：GH=DG
所以：角1=∠2 ，
而∠1=∠4 ， ∠2=∠3=∠5
∴∠4=∠5 ， ∴AF=EF.
end
声明：本文内容来源于网络 ， 转载请联系原出处 。初三研究中心尊重版权 ， 如有侵权问题 ， 请及时与管理员联系处理 。
点击 "阅读原文" 加 中考君微信好友哦