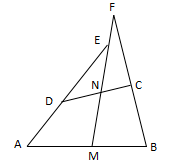
1、已知：如图 ， 在四边形ABCD中 ， AD＝BC ， M、N分别是AB、CD的中点 ， AD、BC的延长线交MN于E、F．求证：∠DEN＝∠F．

文章图片

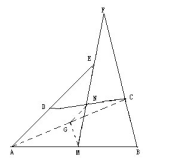
如下图连接AC并取其中点Q ， 连接QN和QM ，

文章图片

所以可得∠QMF=∠F ，
∠QNM=∠DEN和∠QMN=∠QNM ，
从而得出∠DEN＝∠F 。
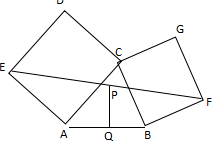
2、如图 ， 分别以△ABC的AC和BC为一边 ， 在△ABC的外侧作正方形ACDE和正方形CBFG ， 点P是EF的中点．求证：点P到边AB的距离等于AB的一半．

文章图片

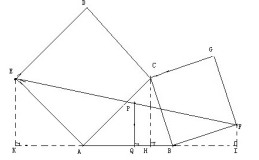
过E,C,F点分别作AB所在直线的高EG ， CI ， FH 。

文章图片

可得PQ=（EG+FH）/2
由△EGA≌△AIC ，
可得EG=AI ， 由△BFH≌△CBI ， 可得FH=BI 。
从而可得PQ=AI+BI/2=AB/2,从而得证 。
3、如图 ， 四边形ABCD为正方形 ， DE∥AC ， AE＝AC ， AE与CD相交于F．求证：CE＝CF．

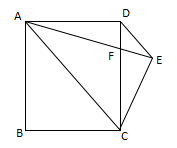
文章图片

顺时针旋转△ADE ， 到△ABG ， 连接CG.

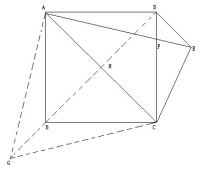
文章图片

由于∠ABG=∠ADE=900+450=1350
从而可得B ， G ， D在一条直线上 ，
【初二数学期末复习：几何经典题含详细解答过程】可得△AGB≌△CGB 。
推出AE=AG=AC=GC ， 可得△AGC为等边三角形 。
∠AGB=300 ， 既得∠EAC=300 ，
从而可得∠A EC=750 。
又∠EFC=∠DFA=450+300=750.
可证：CE=CF 。
4、如图 ， 四边形ABCD为正方形 ， DE∥AC ， 且CE＝CA ， 直线EC交DA延长线于F．
求证：AE＝AF．

文章图片

连接BD作CH⊥DE ， 可得四边形CGDH是正方形 。

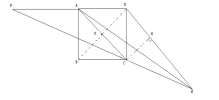
文章图片

由AC=CE=2GC=2CH ，
可得∠CEH=300 ，
所以∠CAE=∠CEA=∠AED=150 ，
又∠FAE=900+450+150=1500 ，
从而可知道∠F=150 ，
从而得出AE=AF 。
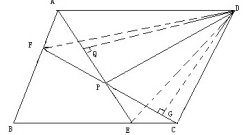
5、平行四边形ABCD中 ， 设E、F分别是BC、AB上的一点 ， AE与CF相交于P ， 且AE＝CF．求证：∠DPA＝∠DPC．

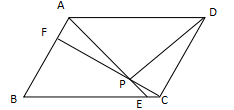
文章图片

过D作AQ⊥AE， AG⊥CF，

文章图片

由S?ADE=□ABCD/2=S?DFC,可得：
AE?PQ/2=AE?PQ/2,由AE=FC.
可得DQ=DG ，
可得∠DPA＝∠DPC（角平分线逆定理） 。
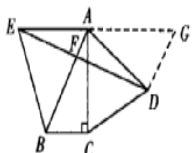
6、如图 ， △ABC中 ， ∠C为直角 ， ∠A=30° ， 分别以AB、AC为边在△ABC的外侧作正△ABE与正△ACD ， DE与AB交于F 。 求证：EF=FD 。

文章图片

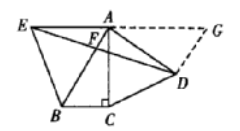
证明：过D作DG//AB交EA的延长线于G ，

文章图片

可得∠DAG=30°
∵∠BAD=30°＋60°=90°∴∠ADG=90°
∵∠DAG=30°=∠CAB ， AD=AC
∴Rt△AGD≌Rt△ABC∴AG=AB ， ∴AG=AE