该证明器在 miniF2F 基准测试中实现了 SOTA（41.2% vs 29.3%）水平 ， miniF2F 包含一组具有挑战性的高中奥林匹克问题 。
研究者将他们的方法称为 statement curriculum learning ， 该方法包括手动收集的一组不同难度级别的命题（无需证明） ， 其中最难的命题类似于目标基准 。 最初 ， 他们的神经证明器很弱 ， 只能证明其中的几个 。 因此 ， 他们迭代地搜索新的证明 ， 并在新发现的证明上重新训练他们的神经网络 。 经过 8 次迭代 ， 他们的证明器在 miniF2F 上取得了出色的成绩 。
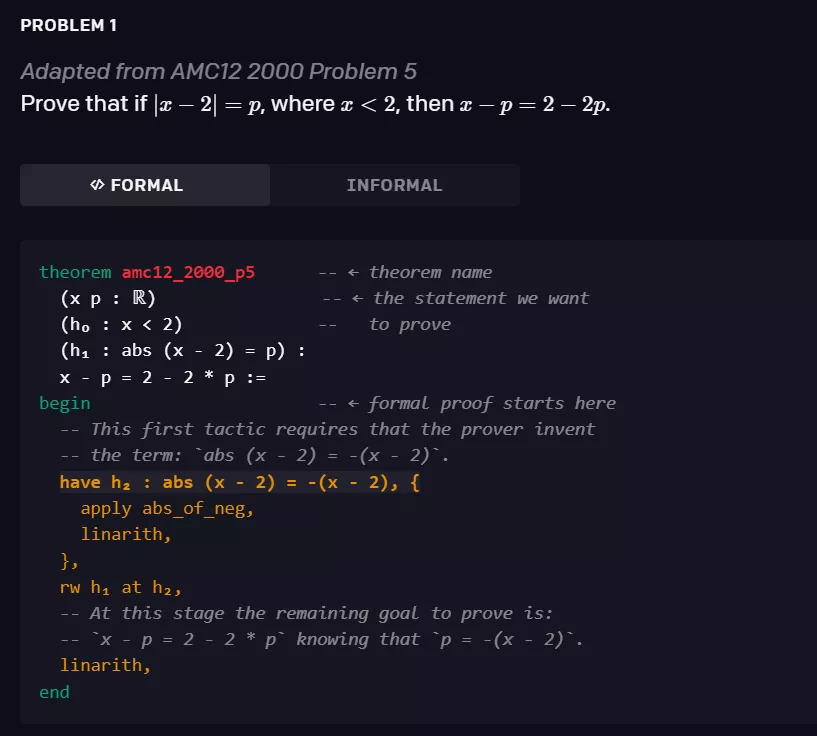
形式化数学（formal mathematics）是一个令人兴奋的研究领域 ， 因为：1）它很丰富 ， 可以让你证明需要推理、创造力和洞察力的任意定理；2）它与游戏相似 ， 也有一种自动化的方法来确定一个证明是否成立（即由形式系统验证） 。 如下图中的例子所示 ， 证明一个形式化的命题需要生成一系列的证明步骤 ， 每个证明步骤都包含对策略（ tactic）的调用 。
形式化系统接受的 artifact 是低级的（就像汇编代码） ， 人类很难产生 。 策略是从更高层次的指令生成这种 artifact 的搜索过程 ， 以辅助形式化 。
这些策略以数学术语作为参数 ， 每次策略调用都会将当前要证明的命题转换为更容易证明的命题 ， 直到没有任何东西需要证明 。

文章图片

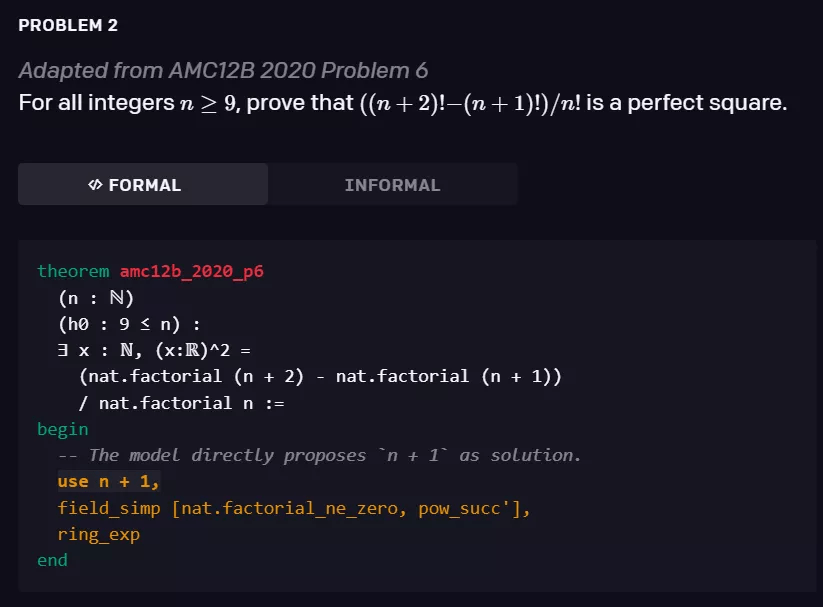
研究者观察到 ， 生成策略参数所需的原始数学术语的能力出现在了他们的训练过程中 ， 这是离开神经语言模型所无法完成的 。 下面的证明就是它的一个例子：证明步骤「use n + 1」（完全由模型生成）提出使用「n + 1」作为解决方案 ， 剩下的形式证明依赖于「ring _ exp」策略来验证它确实有效 。

文章图片

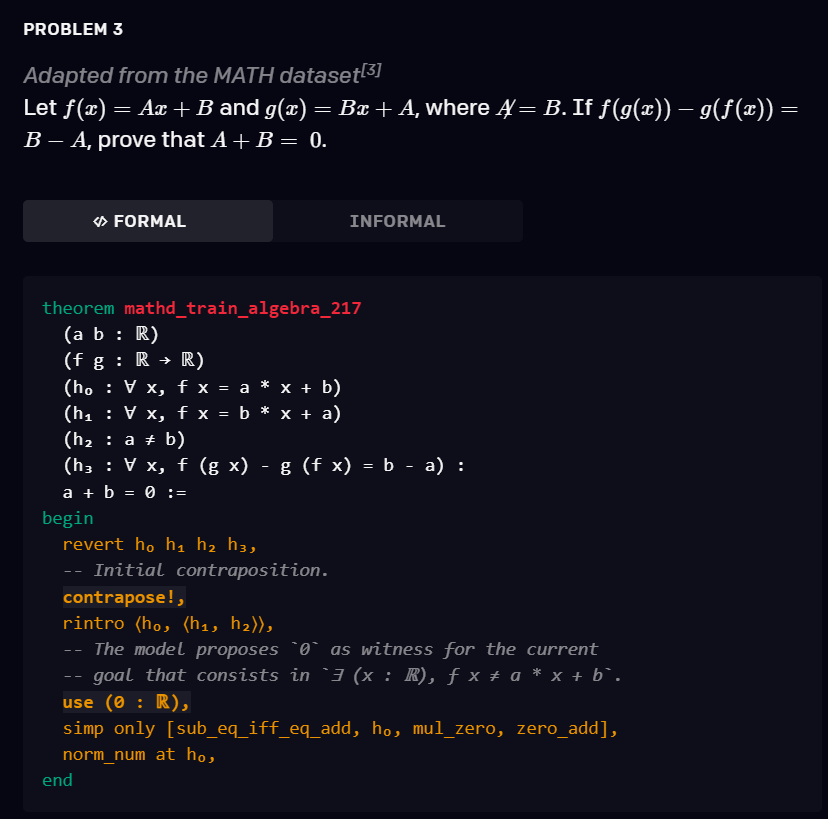
研究者还观察到 ， 他们的模型和搜索过程能够产生链接多个重要推理步骤的证明 。 在下面的证明中 ， 模型首先使用了引出存在性命题（existential statement） (? (x : ?), f x ≠ a * x + b) 的换质换位律（contraposition） 。 然后 ， 它使用 use (0 : ?) 为它生成一个 witness ， 并通过利用 norm _ num 策略来完成证明 。

文章图片

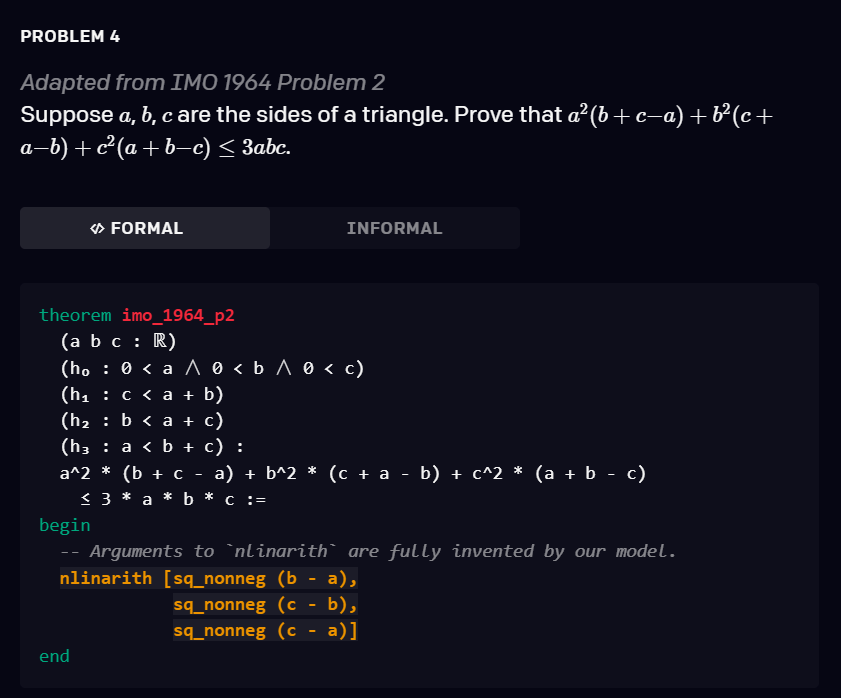
该模型经过 statement curriculum learning 的训练 ， 能够解决培训教材以及 AMC12 和 AIME 中的各种问题 ， 以及改编自 IMO 的两个问题 。 下面是三个有关的例子 。

文章图片


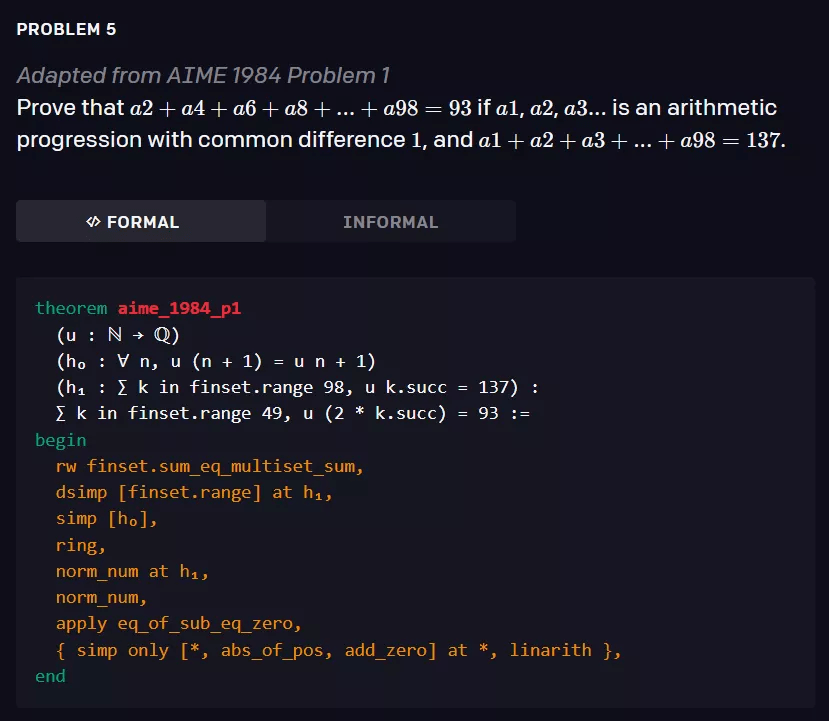
文章图片


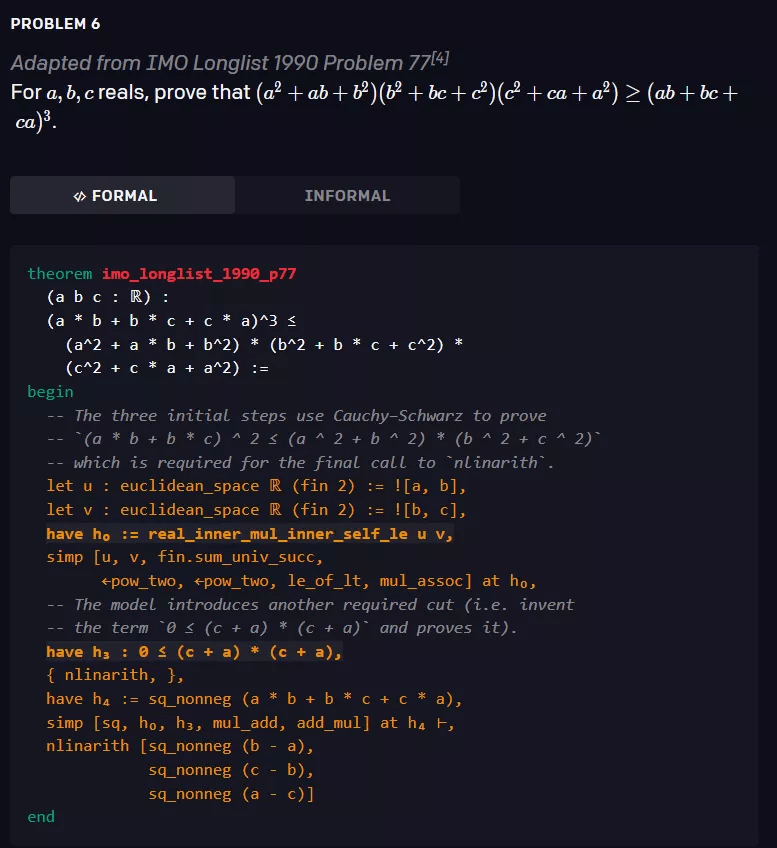
文章图片

形式数学涉及两个主要的挑战 ， 使得单纯的强化学习应用不太可能成功：
1. 无限的动作空间：形式数学不仅有超大的搜索空间（比如像围棋） ， 还有无限的动作空间 。 在搜索证明的每个步骤 ， 模型的选择范围不是一组行为良好的有限动作 ， 而是一组复杂且无限的策略 ， 涉及必须生成的外生数学术语（例如 ， 生成用作 witness 的数学命题) 。
2. 缺乏自博弈（self-play）：与两人游戏相反 ， 证明器不是与对手对抗 ， 而是与一系列需要证明的命题对抗 。 当面对一个过于困难的命题时 ， 没有明显的重构可以让证明器首先生成更容易处理的中间语句 。 这种不对称性阻止了在双人游戏中获得成功的自博弈算法的简单应用 。