论文《Transformer Quality in Linear Time》：

文章图片

论文链接：https://arxiv.org/abs/2202.10447
门控注意力单元
研究者首先提出了门控注意力单元（Gated Attention Unit, GAU） ， 这是一个比 Transformers 更简单但更强的层 。 虽然 GAU 在上下文长度上依然具有二次复杂度 ， 但它在下文展示的近似方法中更可取 。
相关的层包括如下：

• 原版多层感知机（Vanilla MLP）；
• 门控线性单元（Gated Linear Unit, GLU） ， 它是门控增强的改进版 MLP 变体 。 GLU 已被证实在很多情况下都有效 ， 并在 SOTA Transformer 中使用；
• 门控注意力单元（GAU） ， 其核心思路是将注意力和 GLU 作为一个统一层 ， 并尽可能多地共享它们的计算 ， 具体如下图 2 所示 。 这样做不仅实现了更高的参数和计算效率 ， 而且自然地赋能一个强大的注意力门控机制 。

文章图片

【谷歌Quoc Le团队新transformer：线性可扩展，训练成本仅原版1/12】图 2 左为包含两个块的增强 Transformer 层 ， 这两个块分别为门控线性单元（GLU）和多头自注意力（MHSA）；图 2 中为研究者提出的门控注意力单元（GAU）；图 2 右为 GAU 的伪代码 。
研究者在下图 3 中展示了 GAU 与 Transformers 的比较情况 ， 结果显示对于不同模型大小 ， GAU 在 TPUs 上的性能可与 Transformers 竞争 。 需要注意 ， 这些实验是在相对较短的上下文大小（512）上进行的 。

文章图片

下表 1 和表 2 为层消融实验 ， 结果显示 GAU 和 Transformers 各自都是局部最优的 。

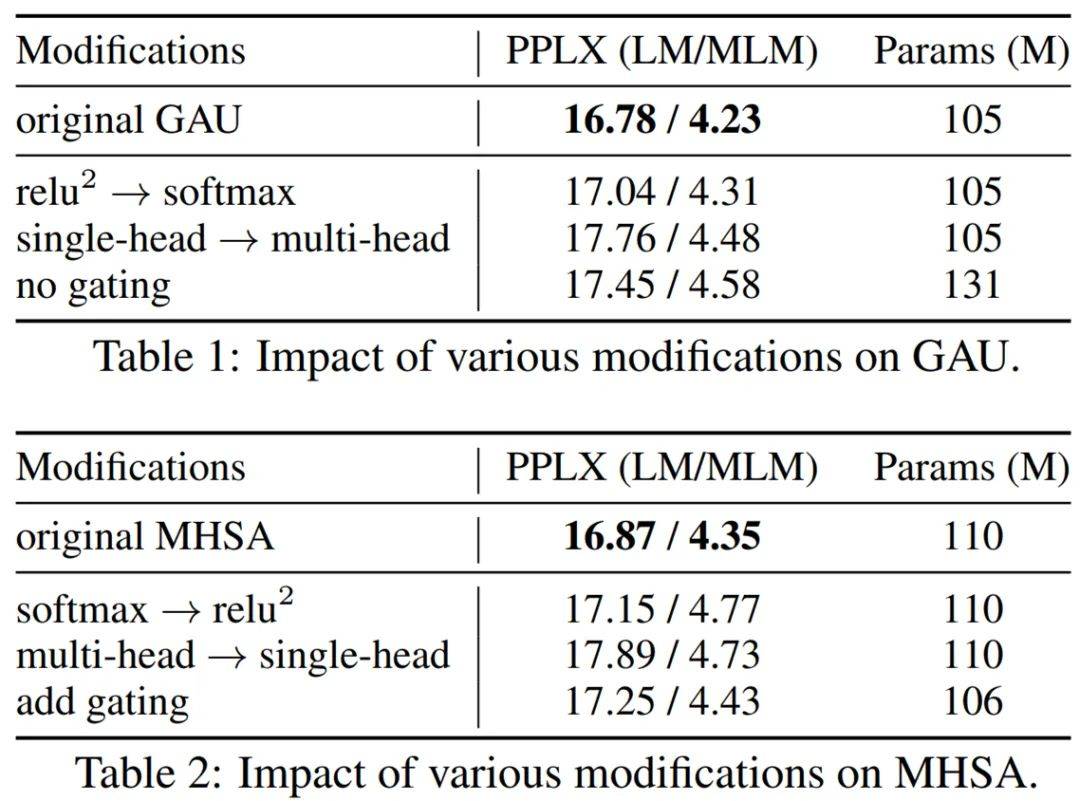
文章图片

使用 GAU 的快速线性注意力（FLASH）
研究者从上一章节得到了以下两个重要的观察结果 ， 并受到启发将 GAU 扩展至建模长序列中 。

• 其一 ， GAU 中的门控机制使得可以使用没有质量损失的更弱的（单头、无 softmax）的注意力 。 如果进一步将这一思路引入到使用注意力建模长序列中 ， GAU 也可以提升近似（弱）注意力机制的有效性 ， 比如局部、稀疏和线性注意力；
• 其二 ， 使用 GAU 使注意力模块的数量自然地增加一倍 ， 就开销而言 ， MLP+MHSA 约等于两个 GAU 。 由于近似注意力通常需要更多层来捕获完整依赖 ， 因此这一特征使得 GAU 更适宜建模长序列 。

研究者首先回顾了使用注意力建模长序列的一些相关工作 ， 然后展示了如何使得 GAU 在长序列上以线性时间实现 Transformer 级别的质量 。 现有的线性复杂度变体（Linear-Complexity Variant）包括局部注意力和线性注意力 。
混合块注意力
根据现有线性复杂度的优缺点 ， 研究者提出了混合块注意力（mixed chunk attention） ， 它融合了局部注意力和线性注意力的优点 。 下图 4 为二次注意力（Quadratic attention）、线性注意力和混合块注意力的构造比较 。

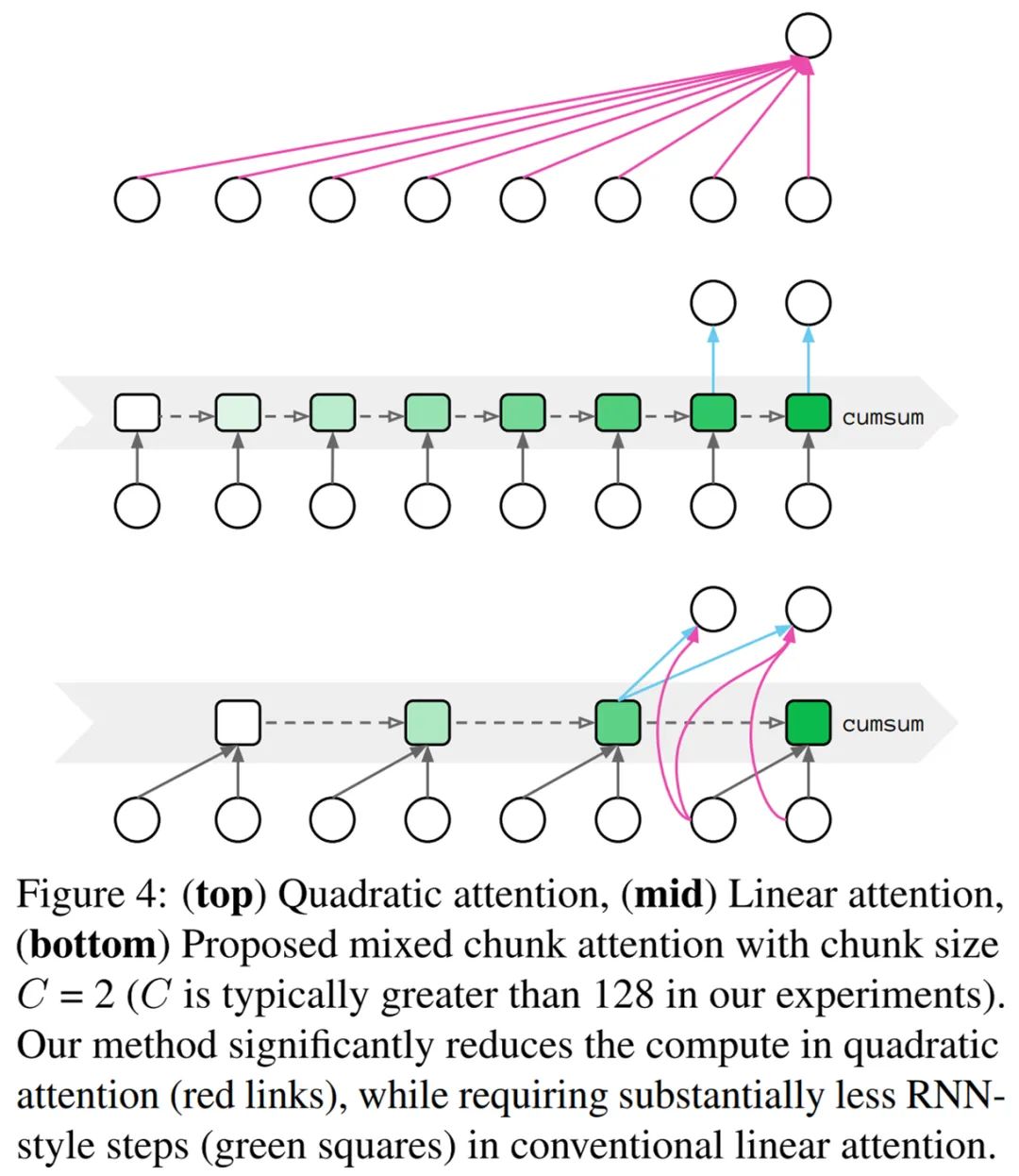
文章图片

输入序列首先被切割成 G 个大小为 C 的非重叠块 ， 也就是

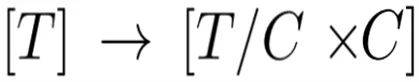
文章图片

。 然后为每个块 g 生成 U_g ? R^C×e、V_g ? R^C×e 和 Z_g ? R^C×s 。
最后使用 per-dim 缩放和偏移来从 Z_g 中生成四种类型的注意力头 ， 即 Q^quad_g、K^quad_g、Q^lin_g 和 K^lin_g 。