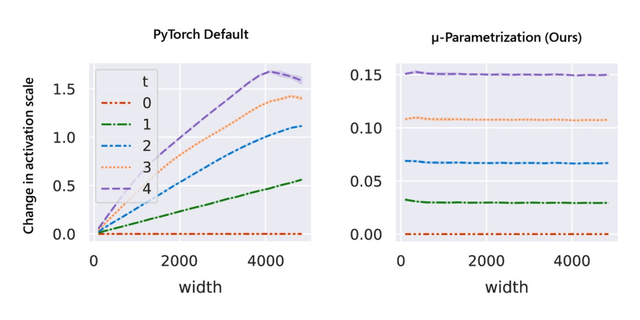
与随机初始化不同 ， 模型训练期间的行为更难进行数学分析 。 该研究用 μP 解决 ， 如图 1 右侧所示 ， 该图显示了网络激活扩展（activation scales）在模型宽度增加的最初几个训练步骤中的稳定性 。

文章图片

图 1：在 PyTorch 的默认参数化中 ， 左图 ， 在经过一次 step 训练后 ， 激活扩展的宽度会出现差异 。 但是在右图的 μP 中 ， 无论训练 step 宽度如何 ， 激活扩展都会发生一致的变化 。
事实上 ， 除了在整个训练过程中保持激活扩展一致之外 ， μP 还确保不同且足够宽的神经网络在训练过程中表现相似 ， 以使它们收敛到一个理想的极限 ， 该研究称之为特征学习极限 。
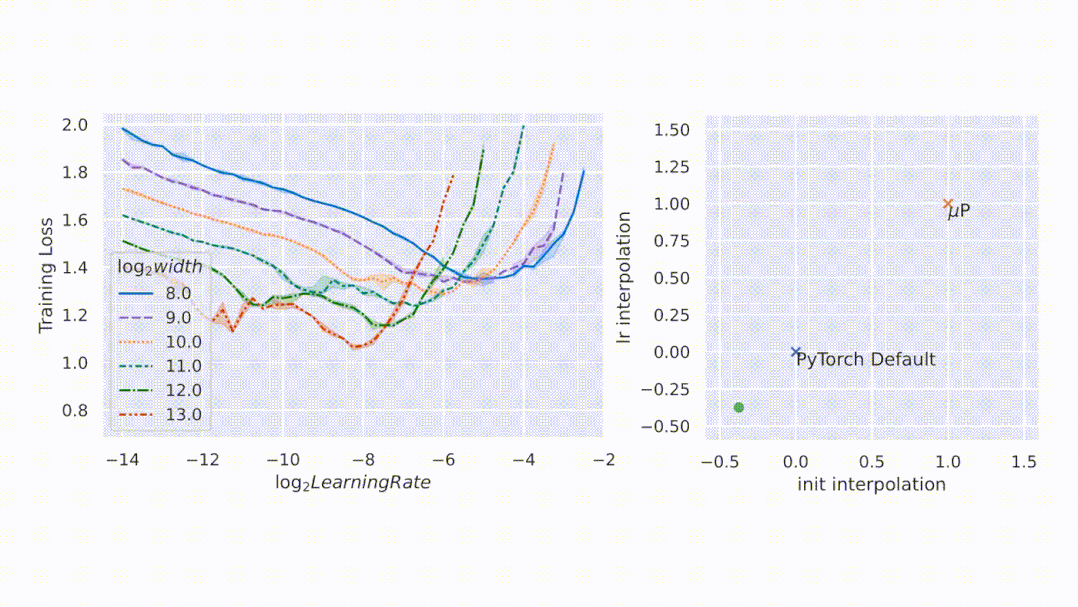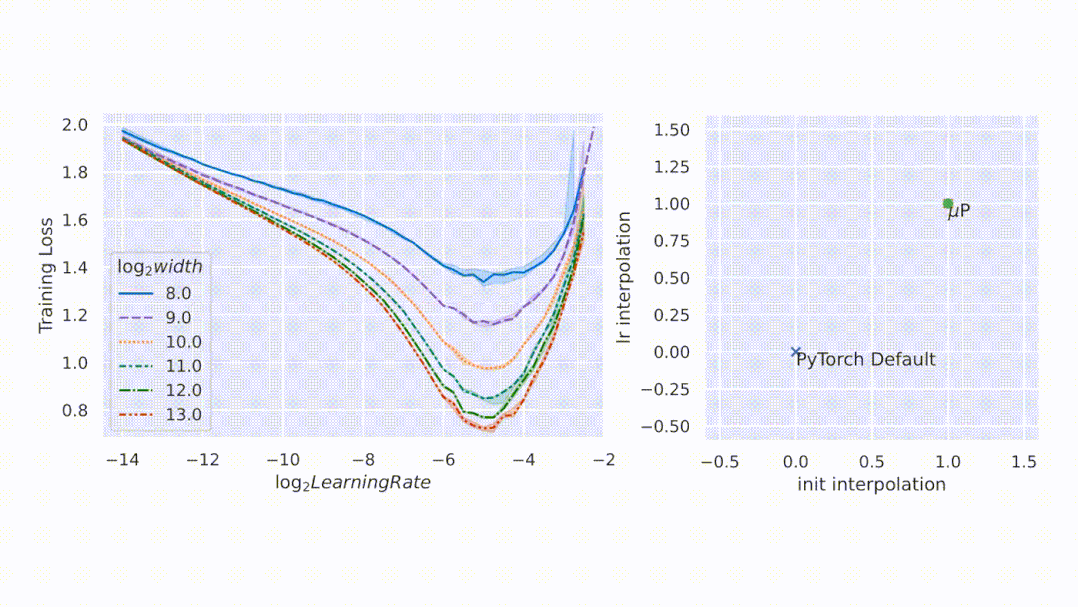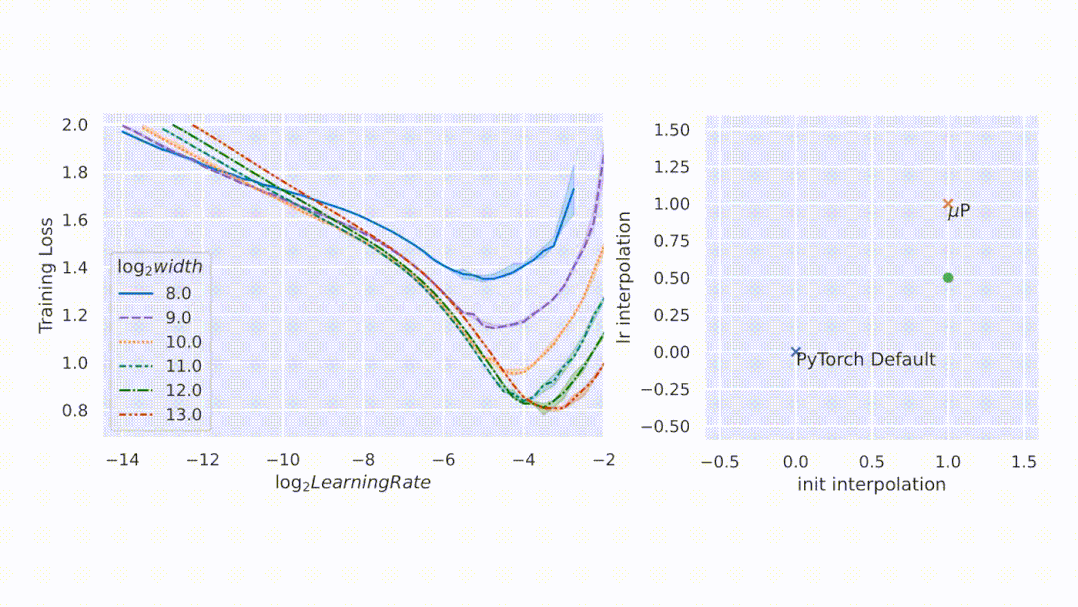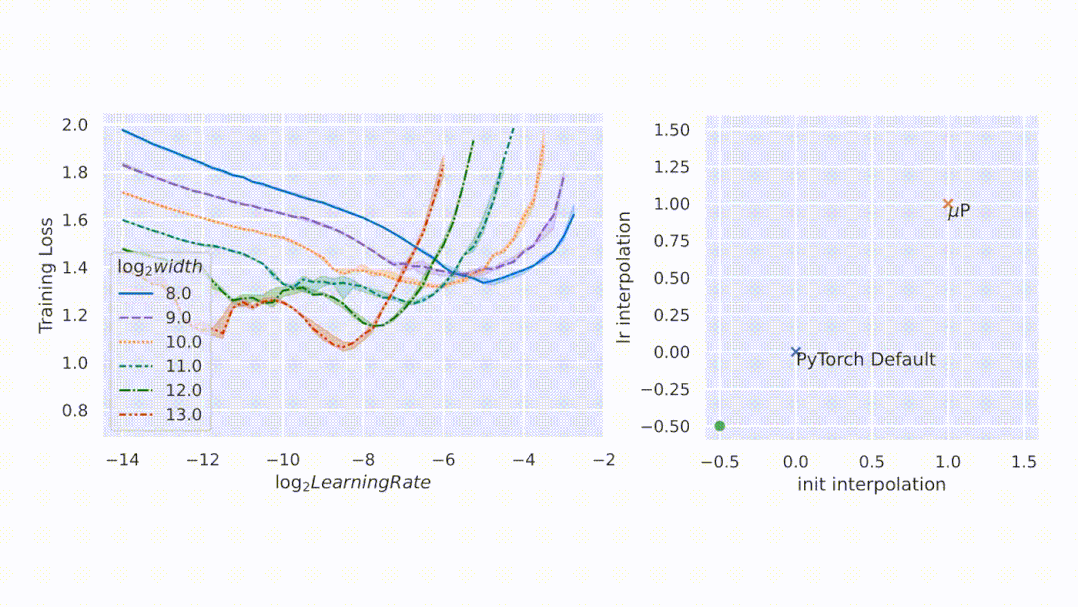
如图所示 ， μP 是唯一在宽度上保持最佳学习率的参数化 ， 在宽度为 213 - 8192 的模型中实现了最佳性能 ， 并且对于给定的学习率 ， 更宽的模型性能更好——即曲线不相交 。

文章图片

图2左侧 ， 该研究在 CIFAR10 上以不同的学习率（沿 x 轴显示）训练不同宽度（对应于不同颜色和图案的曲线）的多层感知器 (MLP) ， 并沿 y 轴绘制训练损失 。 右侧 ， 参数化的 2D 平面由以下插值形成：1）PyTorch 默认值和 μP（x 轴）之间的初始化扩展 ， 以及 2）PyTorch 默认值和 μP（y 轴）之间的学习率扩展 。 在这个平面上 ， PyTorch 默认用 (0,0) 表示 ， μP 默认用 (1,1) 表示 。
基于张量程序（Tensor Programs）的理论基础 ， μTransfer 自动适用于高级架构 ， 例如 Transformer 和 ResNet 。 此外 ， 它还可以同时迁移各种超参数 。
以 Transformer 为例 ， 图 3 展示了关键超参数如何在宽度上保持稳定 。 超参数可以包括学习率、学习率 schedule、初始化、参数乘数等 ， 甚至可以单独针对每个参数张量 。 该研究在最大宽度为 4096 的 Transformer 上验证了这一点 。

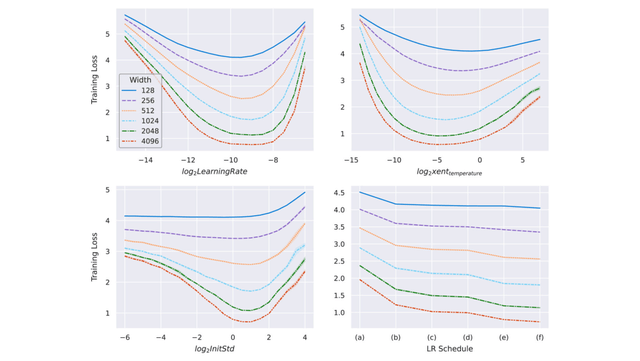
文章图片

图 3：在 μP 中参数化并在 WikiText-2 上训练的不同宽度的 transformer 。 随着模型宽度的增加 ， 最优学习率、交叉熵温度、初始化规模和学习率方案保持稳定 。 查看网络的超参数有助于预测更宽网络的最佳超参数 。 在右下角的图中 ， 该研究尝试了如下学习率方案：(a) 线性衰减 ， (b) StepLR @ [5k, 8k] ， 衰减因子为 0.1 ， (c) StepLR @ [4k, 7k] ， 衰减因子为 0.3 ， (d) 余弦退火 ， (e) 常数 ， (f) 逆平方根衰减 。
模型深度的实验扩展
现代神经网络扩展不止涉及宽度一个维度 。 该研究还探索了如何通过将 μP 与非宽度维度的简单启发式算法相结合 ， 将其应用于现实的训练场景 。 下图 4 使用相同的 transformer 设置来显示最佳学习率如何在合理的非宽度维度范围内保持稳定 。

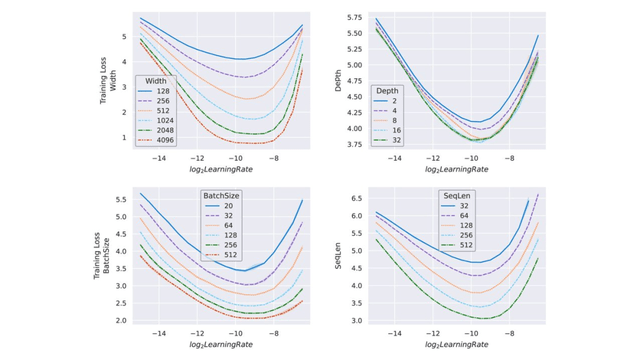
文章图片

图 4：在 μP 中参数化并在 Wikitext-2 上训练的不同大小的 transformer 。 如图 3 所示 ， 最优学习率不仅可以跨宽度迁移 ， 还可在测试范围内实验性地跨其他扩展维度迁移 ， 例如深度、批大小和序列长度 。 这意味着可以将理论上的跨宽度迁移与实验验证的跨其他扩展维度迁移相结合 ， 以获得能在小模型上间接调整超参数并迁移到大模型的 μTransfer 。
除了学习率 ， 其他超参数的情况如下图所示：

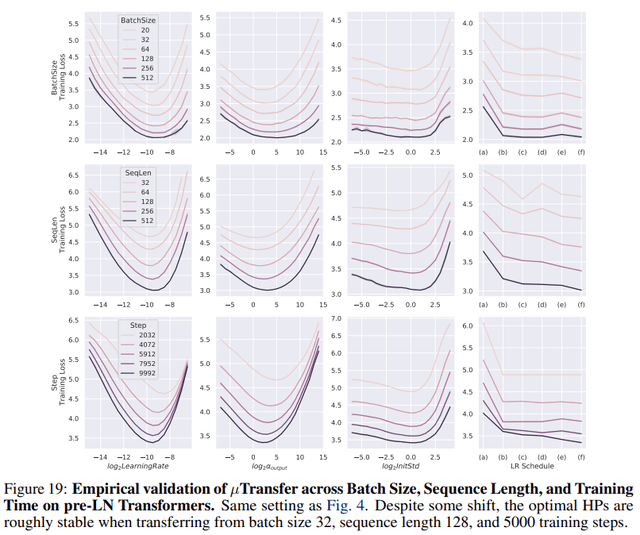
文章图片