测试 μTransfer
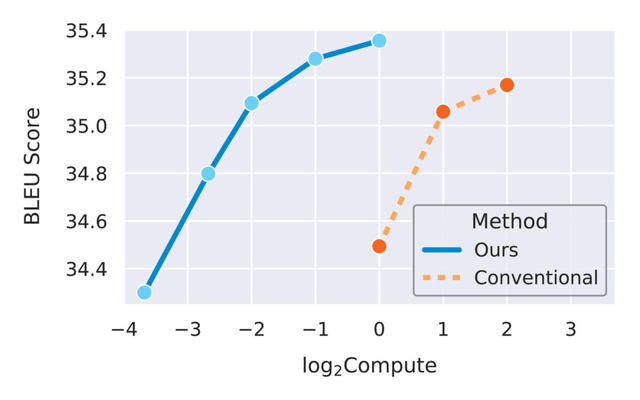
在验证完单个超参数的迁移之后 ， 研究者试图将它们组合到更现实的场景中 。 下图 5 对比了两种情况 ， 一种是 μTransfer 从一个小型 proxy 模型迁移调整过的超参数 ， 另一种是直接调整大型目标模型 。 在这两种情况下 ， 调整都是通过随机搜索完成的 。

文章图片

图 5：μTransfer 大约将计算效率提高了一个数量级 。
由于 proxy 模型即使很小也能有意义地预测最佳超参数（如图 3、图 4 所示） ， 因此随着该研究用数十亿个参数训练更大的目标模型 ， 研究者预计性能差距会扩大 。
未来方向：μP + GPT-3
在这项工作之前 ， 模型越大 ， 调优成本越高 ， 预计调优效果就越差 。 研究者预计 μTransfer 将给最大的模型带来最大的增益 ， 因此该研究与 OpenAI 合作 ， 在 GPT-3 上评估 μTransfer 。
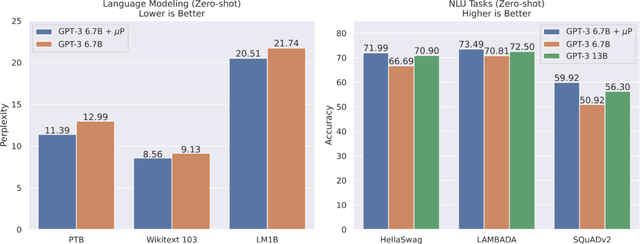
使用 μP 中的相对注意力对 GPT-3 的一个版本进行参数化后 ， 该研究调整了一个具有 4000 万个参数的小型 proxy 模型 ， 然后按照 μTransfer 的方法将最佳超参数组合复制到 GPT-3 的 67 亿参数变体中 。 在此调整阶段使用的总计算量仅为 67 亿模型预训练使用计算量的 7% 。 如下图 6 所示 ， 这个使用 μTransfer 的模型优于 GPT-3 论文中相同大小的模型（绝对注意力） ， 它的性能与 GPT-3 论文中参数数量翻倍的模型（绝对注意力）相当 。

文章图片

理论意义
μP 给出了一个扩展规则 ， 该规则在训练损失方面唯一地保留了跨不同宽度模型的最佳超参数组合 。 相反 ， 其他扩展规则（如 PyTorch 中的默认初始化或 NTK 参数化） ， 随着网络变得越来越宽 ， 超参数空间中的最优值却越来越远 。 研究者认为：实际使用特征学习神经网络时 ， 为了获得适用的见解 ， μP 的特征学习限制会比 NTK 限制更自然 。 因此 ， 过参数化神经网络应该在大型宽度设置中重现 μP 的特征学习限制 。
过去几年开发的张量程序 (TP) 理论使这项进展成为可能 。 TP 理论使研究人员能够计算任何通用计算图在其矩阵维数变大时的极限 。 TP 方法产生了基本的理论结果 ， 例如神经网络 - 高斯过程对应的架构普遍性和动态二分定理 ， 并通过推导 μP 和特征学习限制形成了 μTransfer 。 研究者认为将 TP 理论扩展到深度、批大小等扩展维度是大型模型在宽度之外可靠扩展的关键 。
研究者表示：基础研究是对反复试错的一种高成本效益补充 ， 该研究将继续推导出更具原则性的大规模机器学习方法 。
【单个GPU无法训练GPT-3，但有了这个，你能调优超参数了】参考链接：https://www.microsoft.com/en-us/research/blog/%c2%b5transfer-a-technique-for-hyperparameter-tuning-of-enormous-neural-networks/