文章图片




文章图片




文章图片




文章图片




女士们 ， 先生们 ， 老少爷们儿们！在下张大少 。
本文探讨如何对拼花地板变形中构成边缘的曲线进行美观的演化的问题 。 在正方形拼块简单排列的框架内 ， 我探索了基于网格、迭代函数系统和迷宫路径的曲线演化模型 。
1 引言
拼花变形是威廉·赫夫（William Huff）在60年代初发明的一种平面设计风格[4 ， 第10章
。 每个设计都是一种平面上的 \"空间动画\" ， 是一种拼块沿着一个（有时是两个）维度逐渐演变的过程 。 在一份未发表的手稿[5
中 ， Huff指出了与埃舍尔的变形艺术的美学联系 。 拼花地板的变形旨在成为抽象的形式练习 。 他工作室里的例子都是白色背景上的黑色线条画 。
在以前的工作中[6
， 我研究了与构建拼花变形有关的数学挑战 。 我选择在等面体翻转的背景下看待这个问题 ， 这是一类表现力强但在算法上可操作的由单一形状的副本构成的平面翻转[7
。 给出两个任意的等面体原型 。 我问是否存在一个能在关键帧之间平滑插值的拼块补丁 。 随着两个画格的拼块共享较少的几何属性 ， 我定义了这个问题的一连串越来越难的变化 。
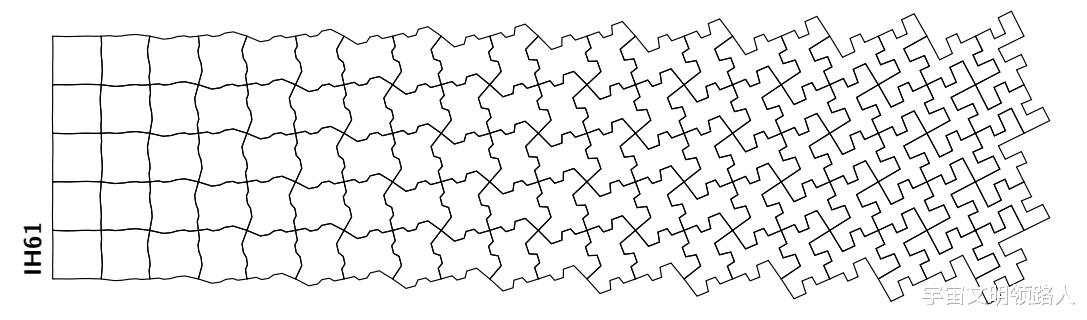
以前的工作主要关注识别对应的边的问题 ， 期望任何插值算法都可以应用于发现的对应边 。 那篇论文中的所有例子都是用一种理想化的算法在两条片状多边形路径之间进行基于长度的线性内插 ， 这种方法的一个例子见图1 。 在本文中 ， 我考虑了一个正交问题 。 也就是说 ， 我假设拼块布局是固定的 ， 边缘对应关系是微不足道的 ， 并专注于不同的可能插值算法和它们提供的美学可能性 。
为了本文的目的 ， 我考虑由拓扑类型（44）的单一等面体拼块（其中所有拼块都是四边形 ， 每个顶点周围都有四面体）构成的拼花变形 。 此外 ， 我将拼块的顶点固定为一个正方形晶格 。 所有这些拼块都可以通过系统地修改 ， 所有这样的密铺都可以通过系统地修改单位方格的无限规则密铺的边来构造 。 我还假定 ， 目标是将原型的最初直边 \"进化 \"为更复杂的形状（而不是在两个任意原型之间变形） 。 在这种情况下 ， 大多数拼块理论的考虑变得微不足道；剩下的就是选择如何进行拼块边缘的演变 。 在这里 ， 我提出了三种有希望的曲线演化的可能性 ， 生成有趣的拼花变形 。 它们是：一种基于网格的、以离散步骤演化的方法（第3节） ， 一种基于迭代函数系统的方法（第4节） ， 以及一种基于迷宫式路径演化的方法（第5节） 。

图1：拼花变形的一个例子 ， 通过一个简单的分段多边形路径的线性插值构造 ， 定义了一个原始拼块的边缘 。 在本文中所有的拼花变形中 ， 图的左侧是等面体拼块类型 。
2拼花地板变形框架
本文中的拼花变形是基于对等面体拼块边缘的操作 ， 其拓扑结构(44)和拼块顶点固定在一个方形晶格中 。 我已经开发了一个软件库 ， 用于表示属于这一类的原型的形状 ， 并用于渲染所产生的变形 。 该库使用先前描述的数据结构和算法[7