03
曲线、运动和变化
无穷原则围绕着方法论主题构建了微积分的故事 。 但微积分既与方法论有关 ， 也与谜题有关 。 最重要的是 ， 有三个谜题促进了微积分的发展 ， 它们分别是曲线之谜、运动之谜和变化之谜 。
一切都始于曲线之谜 。
没有人能算出一个球体的表面积或体积有多大 ， 即使是求圆的周长和面积 ， 在古代也是一个难题 。 人们既不知道该从何处着手 ， 也找不到便于理解的平直部件 。 总之 ， 所有弯曲的东西都难以捉摸 。
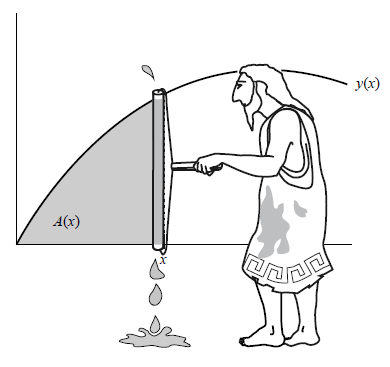
微积分就是在这样的背景下诞生的 ， 它萌生于几何学家对圆度的好奇心和挫败感 。 圆、球体和其他曲线形状是他们那个时代的“喜马拉雅山脉” ， 它们激发了人类的冒险精神 。 就像攀登珠穆朗玛峰的探险家一样 ，几何学家之所以想解决曲线问题 ， 是因为它们就在那里 。

文章图片

有些几何学家坚持认为“曲线事实上是由平直部件构成的” ， 这种观点带来了突破性进展 。 尽管这不是事实 ， 但我们可以假装它是真的 。 那么 ， 唯一的问题就在于 ， 这些部件必须无穷小 ， 而且数量无穷多 。 通过这个巧妙的构思 ， 积分学诞生了 ， 这是人们对无穷原则的最早应用 。 多个世纪以来 ， 世界上最伟大的数学家都在努力探究这个难题的解决办法 。 不过 ， 通过共同的努力（有时还伴有激烈的竞争） ， 他们终于在破解曲线之谜上取得了进展 。

文章图片

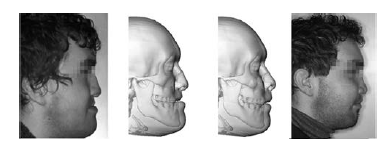
【世界被一种神秘的数学力量彻底改变了】用微积分原理绘制的需下颌手术的患者面部模型（左二）和预测术后效果模型（右二）
之后 ， 人们开始解决第二大谜题 ， 也就是地球上和太阳系中的运动之谜 。
我们将在本书的中间章节里看到 ， 微积分的下一次重大进步源于对运动之谜的探索 。 就像在破解曲线之谜时一样 ， 无穷原则再次挺身而出 。 这一次 ， 我们的创造性假设是 ， 速度不停变化的运动是由无穷多个无限短暂的匀速运动组成的 。
17 世纪中期 ， 微积分的发展时断时续 ， 非常缓慢 ， 代数一部分数学家当作笑话 ， 渐渐失去话语权 。
这时有一个孩子在圣诞节那天出生了——早产儿 ， 没有父亲 ， 3 岁时又被母亲遗弃了 。 想法消沉的孤寂男孩就这样长成了沉默寡言、猜疑心重的年轻人 ， 不过 ， 名叫艾萨克·牛顿的他日后会在世界上留下空前绝后的印记 。
艾萨克·牛顿
他先是通过把代数的符号与无穷的力量结合起来 ， 他找到了一种方法 ， 可以把任何曲线都表示成无穷多条简单曲线（用变量x 的幂来描述 ， 比如x2、x3、x4 等）的和 。 仅用这些“食材” ， 通过加一点儿x、少许x2 和满满一汤匙x3 ， 他就可以“烹饪”出他想要的任何曲线 。 有了它 ， 牛顿就能解决关于形状或运动的任何问题了 。
之后 ， 他破解了宇宙密码 。 他仅用几个微分方程（他的运动和万有引力定律） ， 就能解释包括炮弹的飞行轨迹和行星的运行轨道在内的所有现象 。 牛顿的惊人的“世界体系”统一了天和地 ， 掀起了启蒙运动 ， 改变了西方文化 ，对欧洲的哲学家和诗人产生了巨大的影响 。 他甚至影响了托马斯·杰斐逊和《独立宣言》的起草 。

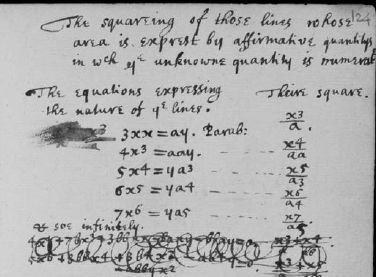
文章图片

牛顿手稿
在破解了曲线之谜和运动之谜后 ， 微积分转向了它的第三个由来已久的谜题——变化之谜 。