比如刚刚那个电影评分的例子中 ， 预测那些没有被评分的电影的分数只依赖于已经打分的那些分数 ， 并不需要去学习那些电影的特征 。
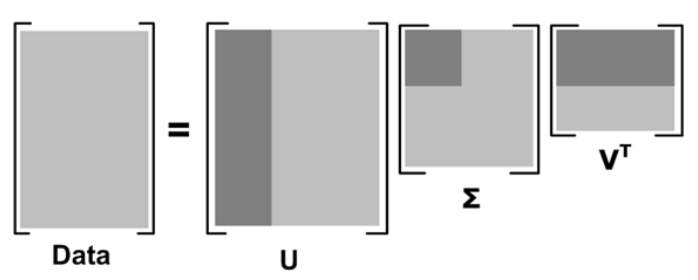
SVD将矩阵分解为三个矩阵的乘积 ， 公式如下所示：
中间的矩阵sigma为对角矩阵 ， 对角元素的值为Data矩阵的奇异值(注意奇异值和特征值是不同的) ， 且已经从大到小排列好了 。 即使去掉特征值小的那些特征 ， 依然可以很好的重构出原始矩阵 。 如下图所示：

文章图片

其中更深的颜色代表去掉小特征值重构时的三个矩阵 。
果m代表商品的个数 ， n代表用户的个数 ， 则U矩阵的每一行代表商品的属性 ， 现在通过降维U矩阵（取深色部分）后 ， 每一个商品的属性可以用更低的维度表示（假设为k维） 。 这样当新来一个用户的商品推荐向量X ， 则可以根据公式X'*U1*inv(S1)得到一个k维的向量 ， 然后在V’中寻找最相似的那一个用户（相似度测量可用余弦公式等） ， 根据这个用户的评分来推荐（主要是推荐新用户未打分的那些商品） 。
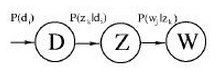
pLSA：由LSA发展过来 ， 而早期LSA的实现主要是通过SVD分解 。 pLSA的模型图如下

文章图片

公式中的意义如下：

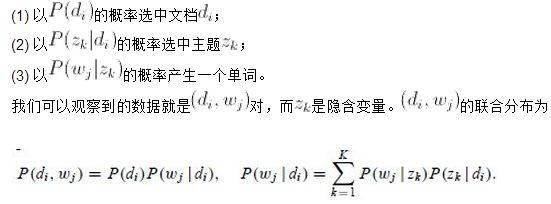
文章图片

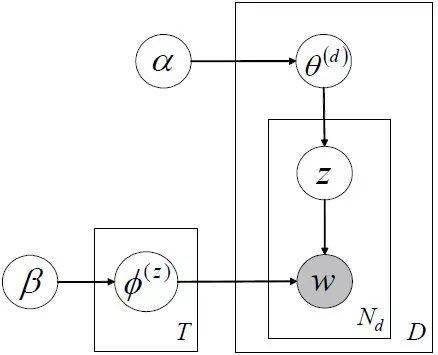
LDA主题模型 ， 概率图如下：

文章图片

和pLSA不同的是LDA中假设了很多先验分布 ， 且一般参数的先验分布都假设为Dirichlet分布 ， 其原因是共轭分布时先验概率和后验概率的形式相同 。
GDBT：GBDT(Gradient Boosting Decision Tree) 又叫 MART（Multiple Additive Regression Tree) ， 好像在阿里内部用得比较多（所以阿里算法岗位面试时可能会问到） ， 它是一种迭代的决策树算法 ， 该算法由多棵决策树组成 ， 所有树的输出结果累加起来就是最终答案 。
它在被提出之初就和SVM一起被认为是泛化能力（generalization)较强的算法 。 近些年更因为被用于搜索排序的机器学习模型而引起大家关注 。
GBDT是回归树 ， 不是分类树 。 其核心就在于 ， 每一棵树是从之前所有树的残差中来学习的 。 为了防止过拟合 ， 和Adaboosting一样 ， 也加入了boosting这一项 。
Regularization作用是
1. 数值上更容易求解；
2. 特征数目太大时更稳定；
3. 控制模型的复杂度 ， 光滑性 。 复杂性越小且越光滑的目标函数泛化能力越强 。 而加入规则项能使目标函数复杂度减小 ， 且更光滑 。
4. 减小参数空间；参数空间越小 ， 复杂度越低 。
5. 系数越小 ， 模型越简单 ， 而模型越简单则泛化能力越强（Ng宏观上给出的解释） 。
6. 可以看成是权值的高斯先验 。
异常检测：可以估计样本的密度函数 ， 对于新样本直接计算其密度 ， 如果密度值小于某一阈值 ， 则表示该样本异常 。 而密度函数一般采用多维的高斯分布 。
如果样本有n维 ， 则每一维的特征都可以看作是符合高斯分布的 ， 即使这些特征可视化出来不太符合高斯分布 ， 也可以对该特征进行数学转换让其看起来像高斯分布 ， 比如说x=log(x+c), x=x^(1/c)等 。 异常检测的算法流程如下：

文章图片

其中的ε也是通过交叉验证得到的 ， 也就是说在进行异常检测时 ， 前面的p(x)的学习是用的无监督 ， 后面的参数ε学习是用的有监督 。 那么为什么不全部使用普通有监督的方法来学习呢（即把它看做是一个普通的二分类问题）？