文章图片

由于高斯的工作 ， 正态分布在误差分析中迅速确定了自己的地位 。 有了这么好的工具 ， 我们可能拍脑袋就认为 ， 正态分布很快就被人们用来分析其它的数据 ， 然而事实却出乎我们的意料 ， 正态分布进入社会领域和自然科学领域 ， 可是经过一番周折的 。
首先我要告诉大家一个事实：误差分析和统计学是两个风马牛不相及的两个学科；当然这个事实存在的时间是19世纪初之前 。 统计学的产生最初与“编制国情报告”有关 ， 主要服务于政府部门 。 统计学面对的是统计数据 ， 是对多个不同对象的测量；而误差分析研究的是观测数据 ， 是对同一个对象的多次测量 。 因此观测数据和统计数据在当时被认为两种不同行为获取得到的数据 ， 适用于观测数据的规律未必适用于统计数据 。 19世纪的统计数据分析处于一个很落后的状态 ， 和概率论没有多少结合 。 而概率论的产生主要和赌博相关 ， 发展过程中与误差分析紧密联系 ， 而与当时的统计学交集非常小 。 将统计学与概率论真正结合起来推动数理统计学发展的便是我们的统计学巨星凯特勒 。
凯特勒这名字或许不如其它数学家那么响亮 ， 估计很多人不熟悉 ， 所以有必要介绍一下 。 凯特勒是比利时人 ， 数学博士毕业 ， 年轻的时候曾追随拉普拉斯学习过概率论 。 此人学识渊博 ， 涉猎广泛 ， 脑门上的桂冠包括统计学家、数学家、天文学家、社会学家、国际统计会议之父、近代统计学之父、数理统计学派创始人 。 凯特勒的最大的贡献就是将法国的古典概率引入统计学 ， 用纯数学的方法对社会现象进行研究 。
1831年 ， 凯特勒参与主持新建比利时统计总局的工作 。 他开始从事有关人口问题的统计学研究 。 在这种研究中 ， 凯特勒发现,以往被人们认为杂乱无章的、偶然性占统治地位的社会现象 ， 如同自然现象一样也具有一定的规律性 。 凯特勒搜集了大量关于人体生理测量的数据 ， 如体重、身高与胸围等 ， 并使用概率统计方法来对数据进行数据分析 。 但是当时的统计分析方法遭到了社会学家的质疑 ， 社会学家们的反对意见主要在于：社会问题与科学实验不同 ， 其数据一般由观察得到 ， 无法控制且经常不了解其异质因素 ， 这样数据的同质性连带其分析结果往往就有了问题 ， 于是社会统计工作者就面临一个如何判断数据同质性的问题 。 凯特勒大胆地提出：

文章图片

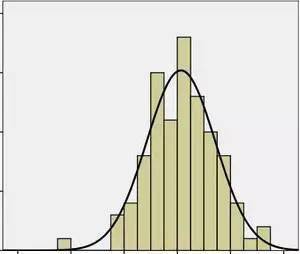
【把一批数据是否能很好地拟合正态分布 ， 作为判断该批数据同质的标准 。 】
凯特勒提出了一个使用正态曲线拟合数据的方法 ， 并广泛的使用正态分布去拟合各种类型的数据 。 由此 ， 凯特勒为正态分布的应用拓展了广阔的舞台 。 正态分布如同一把屠龙刀 ， 在他的带领下 ， 学者们挥舞着这把宝刀在各个领域披荆斩棘 ， 攻陷了人口、领土、政治、农业、工业、商业、道德等社会领域 ， 并进一步攻占天文学、数学、物理学、生物学、社会统计学及气象学等自然科学领域 。
正态分布的下一个推动力来自生物学家高尔顿 ， 当正态分布与生物学联姻时 ， 近代统计学迎来了一次大发展 。 高尔顿是生物统计学派的奠基人 ， 他的表哥达尔文的巨著《物种起源》问世以后 ， 触动他用统计方法研究遗传进化问题 。 受凯特勒的启发 ， 他对正态分布怀有浓厚的兴趣 ， 开始使用正态分布去拟合人的身高、胸围、以至考试成绩等各类数据 ， 发现正态分布拟合得非常好 。 他因此相信正态曲线是适用于无数情况的一般法则 。