然而 ， 对高尔顿而言 ， 这个无处不在的正态性给他带来一些困惑 。 他考察了亲子两代的身高数据 ， 发现遵从同一的正态分布 ， 遗传作为一个显著因素是如何发挥作用的？1877年 ， 高尔顿设计了一个叫高尔顿钉板(quincunx,或者Galton board)的装置 ， 模拟正态分布的性质用于解释遗传现象 。
如下图中每一点表示钉在板上的一颗钉子 ， 它们彼此的距离均相等 。 当小圆球向下降落过程中 ， 碰到钉子后皆以1/2的概率向左或向右滚下 。 如果有n排钉子 ， 则各槽内最终球的个数服从二项分布B(n,1/2),当n较大的时候 ， 接近正态分布 。

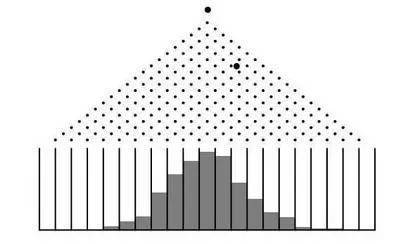
文章图片

【高尔顿钉板】
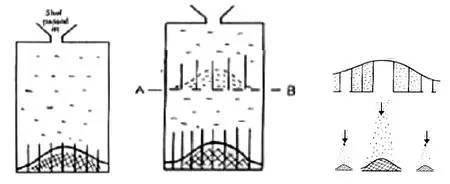
设想在此装置的中间某个地方AB设一个挡板把小球截住 ， 小球将在AB处聚成正态曲线形状 ， 如果挡板上有许多阀门 ， 打开一些阀门 ， 则在底部形成多个大小不一的正态分布 ， 而最终的大正态分布正式这些小正态分布的混合 。

文章图片

【高尔顿钉板解释遗传现象】
高尔顿利用这个装置创造性的把正态分布的性质用于解释遗传现象 。 他解释说身高受到显著因素和其它较小因素的影响 ， 每个因素的影响可以表达为一个正态分布 。 遗传作为一个显著因素 ， 类似图中底部大小不一的正态分布中的比较大的正态分布 ， 而多个大小不一正态分布累加之后其结果仍然得到一个正态分布 。
高尔顿在研究身高的遗传效应的时候 ， 同时发现一个奇特的现象：高个子父母的子女 ， 其身高有低于其父母身高的趋势 ， 而矮个子父母的子女 ， 其身高有高于其父母的趋势 ， 即有“回归”到普通人平均身高去的趋势 ， 这也是“回归”一词最早的含义 。 高尔顿用二维正态分布去拟合父代和子代身高的数据 ， 同时引进了回归直线、相关系数的概念 ， 从而开创了回归分析这门技术 。
可以说 ， 高尔顿是用统计方法研究生物学的第一人 ， 他用实际行动开拓了凯特勒的思想；为数理统计学的产生奠定了基础 。 无论是凯特勒还是高尔顿 ， 他们的统计分析工作都是以正态分布为中心的 ， 在他们的影响下 ， 正态分布获得了普遍认可和广泛应用 ， 甚至是被滥用 ， 以至有些学者认为19世纪是正态分布在统计学中占统治地位的时代 。
6.3 数理统计三剑客
最后 ， 我们来到了20世纪 ， 正态分布的命运如何呢？如果说19世纪是正态分布在统计学中独领风骚的话 ， 20世纪则是数理统计学蓬勃发展、百花齐放的时代 。 1901年 ， 高尔顿和他的学生卡尔·皮尔逊(Karl Pearson)、韦尔登（W.F.R Weldon)创办《生物计量》(Biometrika)杂志 ， 成为生物统计学派的一面旗帜 ， 引导了现代数理统计学的大发展 。 统计学的重心逐渐由欧洲大陆向英国转移 ， 使英国在以后几十年数理统计学发展的黄金时代充当了领头羊 。
在20世纪以前 ， 统计学所处理的数据一般都是大量的、自然采集的 ， 所用的方法以拉普拉斯中心极限定理为依据 ， 总是归结到正态 。 到了19世纪末期 ， 数据与正态拟合不好的情况也日渐为人们所注意：进入20世纪之后 ， 人工试验条件下所得数据的统计分析问题 ， 日渐被人们所重视 。 由于试验数据量有限 ， 那种依赖于近似正态分布的传统方法开始招致质疑 ， 这促使人们研究这种情况下正确的统计方法问题 。
在这个背景之下 ， 统计学三大分布χ2分布、t分布、F分布逐步登上历史舞台 。 这三大分布现在的理科本科生都很熟悉 。 在历史上 ， 这三个分布和来自英国的现代数理统计学的三大剑客有着密切的关系 。