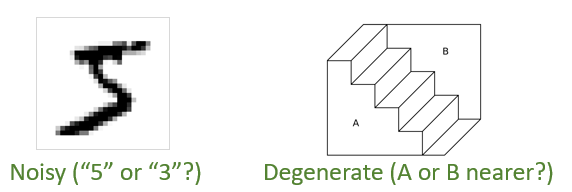
作为对比 ， 当前主流的领域自适应和领域泛化方法会在不同领域上使用同一个编码器来推断隐因子 。 这其实蕴含着“ 推断不变性”（inference invariance） 。 研究员们认为 ，推断不变性是因果不变性的特例 。 在支持推断不变性的例子中 ， 比如从图片中推断物体位置 ， 具有因果性的生成机制 p(x│s,v) 几乎是确定性的且可逆的 ， 意味着只有一个“物体位置”的值（s 的一个分量）才能让 p(x│s,v) 对于给定的 x 非零 。 由于 p(x│s,v) 具有因果不变性 ， 所以这种推断方式便也具有不变性 。 但当 p(x│s,v) 有噪或退化时 ， 仅依据 p(x│s,v) 做推断是任意的 ， 例如图3左图中的数字可能是由“5”也可能是由“3”产生的 ， 而右图中 ， 靠近我们的不论是 A 还是 B 面都会得到同样的图 。 这种情况下 ， 由贝叶斯公式 p(s,v│x)∝p(s,v)p(x│s,v) 给出的推断结果便会明显受到先验的影响 。 而先验是会随环境变化的（对可能的推断结果的偏好因人而异） ， 所以 推断不变性不再成立 ， 而因果不变性却仍然可靠 。

文章图片

图3：当生成机制 p(x│s,v) 有噪（左）或退化（右）时 ， 推断结果具有任意性 ， 因而推断不变性不再可靠
基于因果不变性 ， 研究员们给出了在测试域（test domain）上进行预测的原则 。 本篇论文考虑了两种分布外预测任务 ， 称为“ 分布外泛化”（out-of-distribution generalization）以及“ 领域自适应”（domain adaptation） 。 两者都只有一个训练域（training domain）（因而分布外泛化不同于领域泛化；下一篇工作会解决领域泛化任务） ， 但领域自适应中有测试域上的无监督数据 ， 而在分布外泛化中则对测试域一无所知 。
由因果不变性可知 ， 在测试域上 ， 具有因果性的数据生成机制 p(x│s,v) 和 p(y│s) 仍然适用 ， 但先验分布会发生变化 。 对于分布外泛化则需要考虑测试域先验的所有可能性 。 因此 ， 研究员们提出了适用一个独立的先验分布 p^⊥ (s,v)?p(s)p(v) ， 其中 p(s) 和 p(v) 都是训练域先验 p(s,v) 的边缘分布 。 此选择去掉了 s 和 v 在训练域上的虚假关联（spurious correlation） ， 并且由于 p^⊥ (s,v) 具有比 p(s,v) 更大的熵 ， 因此减去了独属训练域的信息 ， 从而让模型更依赖于具有因果不变性的生成机制进行预测 。 这种预测方法被称为 CSG-ind 。 对于领域自适应 ， 可利用无监督数据学习测试域的先验 p ?(s,v) 用于预测 ， 其对应方法称为 CSG-DA 。 这两个模型示于图2(b,c)中 。 值得注意的是 ， 由于 CSG 在测试域上使用了与训练域不同的先验分布 ， 在测试域上得到的预测规则 p(y│x) 会不同于训练域上的 ， 因而此方法与基于推断不变性的方法严格不同 。
方法
事实上 ， 无论哪种方法都首先需要很好地拟合训练数据 ， 因为这是所有监督信息的来源 。 由于 CSG 涉及隐变量 ， 难以直接计算数据对数似然 log?p(x,y) 用于训练 ， 所以研究员们采用了变分贝叶斯方法（Variational Bayes）优化一个可以自适应变紧的下界 ， 记为ELBO（Evidence Lower BOund） 。 虽然标准做法要引入形如 q(s,v│x,y) 的推断模型（inference model） ， 但它却并不能帮助进行预测 。 为此 ， 研究员们考虑用一个形如 q(s,v,y│x) 的模型表示所需推断模型 q(s,v│x,y)=q(s,v,y│x)/∫q(s,v,y│x) dsdv 。 进一步 ， 将它代入 ELBO 中可发现 ， 这个新的 q(s,v,y│x) 模型的目标正是由 CSG 模型所定义的对应分布 p(s,v,y│x) ， 而由 CSG 的图结构 ， 这个分布可分解为 p(s,v,y│x)=p(s,v│x)p(y│s) ， 其中的 p(y│s) 已由 CSG 模型显式给出 ， 只有 p(s,v│x) 是难以计算的项 。 因此研究员们最终采用了一个形如 q(s,v│x) 的推断模型以近似这个最小的难算部分 p(s,v│x) ， 代入 ELBO 中即得训练目标 。