【如何利用剪枝方法设计更好的决策树】译者 | 李睿
决策树(DT)是一种有监督的机器学习算法 , 用于解决分类和回归问题 。 以下了解一下如何使用剪枝(Pruning)方法设计一个决策树 。

文章图片
决策树分析是一种通用的、预测性的机器学习建模工具 。 它是机器学习最简单、最有用的结构之一 , 通过使用一种根据不同条件拆分数据集的算法方法构建了决策树 。 而决策树是监督学习中常用的功能性技术之一 。
但在采用剪枝方法设计决策树之前 , 需要了解它的概念 。
理解决策树 决策树是一种有监督的机器学习算法 , 用于解决分类和回归问题 。 决策树遵循一组嵌套的if-else语句条件来进行预测 。 由于决策树主要用于分类和回归 , 因此用于生长它们的算法称为CART(分类和回归树) 。 并且提出了多种算法来构建决策树 。 决策树旨在创建一个模型 , 通过学习从数据特征推断出的简单决策规则来预测目标变量的值 。
决策树的每个节点代表一个决策 。
文章图片
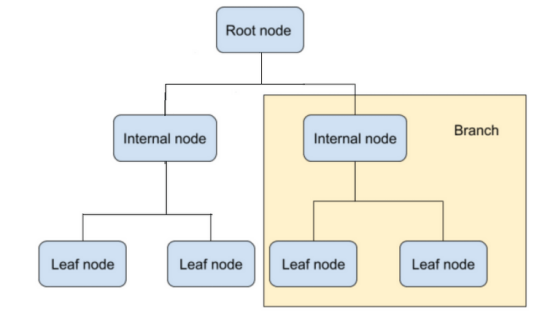
在上图中 , 根节点是深度为零的决策树图的起点 。 然后是进行二叉决策的子节点/内部节点 。 最后 , 还有叶节点 , 用于对类别进行预测 。
有助于构建决策树的算法旨在从变量及其属性中预测目标变量 。 决策树的结构是通过从根节点到分支的二叉序列进行分割的 。 内容要到达决策树中的叶节点 , 必须传递多个内部节点来检查所做的预测 。
构建决策树时的假设 使用决策树时必须做出的一些假设是:
- 整个训练集是根 。
- 最好有分类特征值 。 在构建决策树模型之前使用离散值 。
- 属性值用于递归分发记录 。
- 统计方法用于确定应将哪些属性放置为决策树的根节点或内部节点 。
一个类中的每个分支 , 从根到具有不同分支结尾的决策树的叶节点形成一个析取(和) , 同一个类则形成值的合取(乘积) 。
为什么选择决策树? 决策树遵循与人类在现实生活中做出决策相同的过程 , 使其更易于理解 。 这对于解决机器学习中的决策问题至关重要 。 它普遍用于训练机器学习模型的原因是因为决策树有助于思考问题的所有可能结果 。 此外 , 与其他算法相比 , 对数据清理的要求更少 。
但是 , 决策树也有它的局限性 , 那就是过拟合 。
决策树中的过拟合 过拟合是决策树中的一个重要的难题 。 如果允许决策树增长到最大深度 , 它将总是过拟合训练数据 。 当决策树被设计为完美拟合训练数据集中的所有样本时 , 就会发生过拟合 。 因此 , 决策树最终会产生具有严格稀疏数据规则的分支 , 这会通过使用不属于训练集的样本来影响预测的准确性 。 决策树越深 , 决策规则序列就越复杂 。 而分配最大深度是简化决策树和处理过拟合的最简单方法 。
但是如何以更精确的方式改进决策树模型呢?以下进行一下了解 。
如何通过剪枝防止决策树中的过拟合? 剪枝是一种用于消除决策树中过拟合的技术 。 它通过消除最弱规则来简化决策树 , 可以进一步分为:
- 预剪枝是指通过设置约束来限制决策树在早期阶段的生长 。 为此 , 可以使用超参数调整来设置min_samples_split、min_samples_leaf或max_depth等参数 。
- 在构建决策树之后使用后剪枝方法 。 当决策树变得非常深入并显示模型过拟合时使用它 。 为此 , 还将通过成本复杂性剪枝来控制决策树分支 , 例如max_samples_split和max_depth 。
特别声明:本站内容均来自网友提供或互联网,仅供参考,请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系,我们将在24小时内删除。
