因为我们正把所有的时间都花费在内存带宽上 ， 这种运算也被称作内存限制运算（memory-bound operation） ， 它意味着我们没有把大量时间花费在计算上 。
显然 ， 这并不是我们想要的 。 那我们能做什么呢？让我们来看看算子序列长什么样子 。

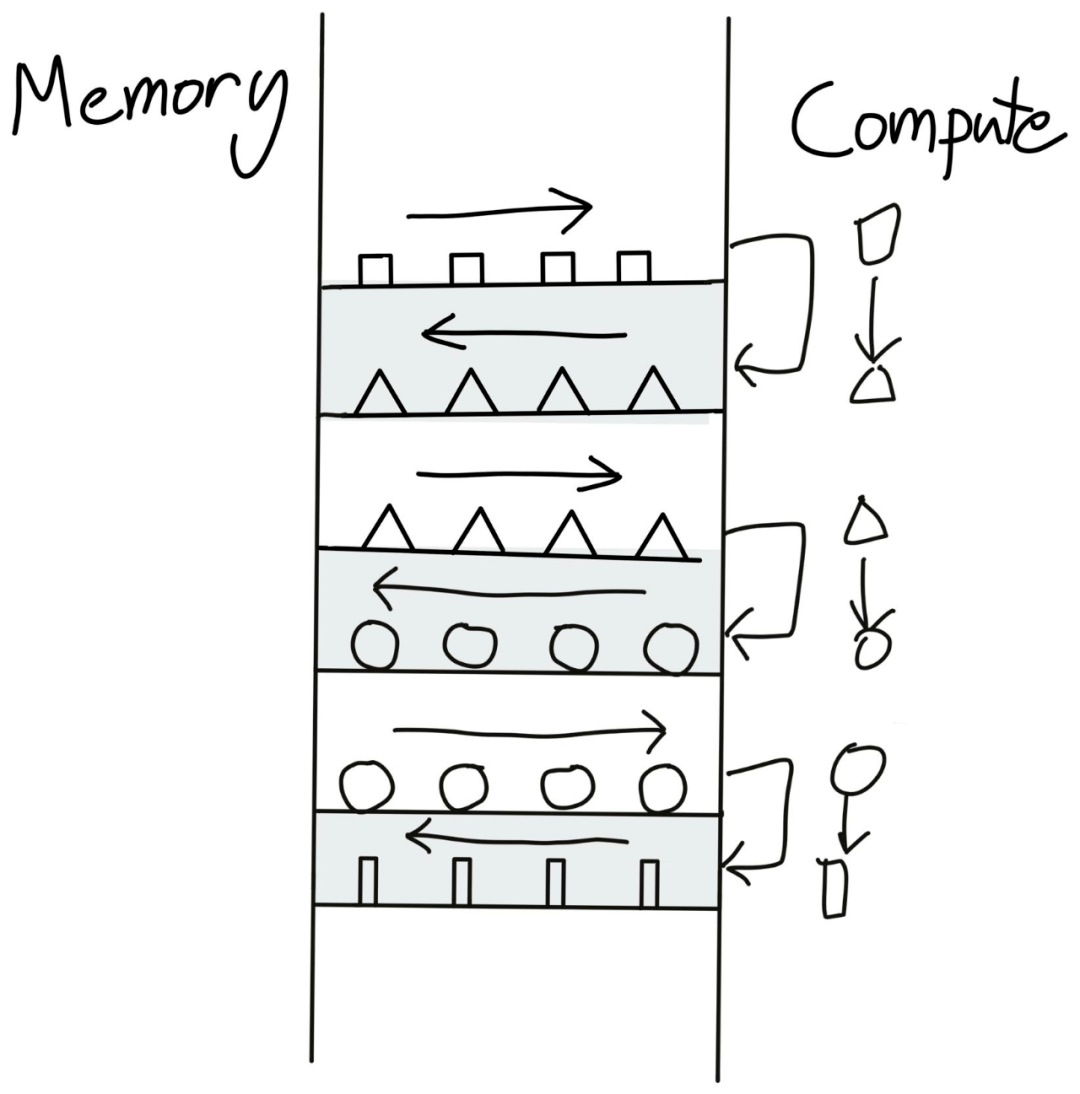
文章图片

【用什么tricks能让模型训练得更快？先了解下这个问题的第一性原理】一个逐点算子序列可能的样子 。
在全局内存和计算单元之间来回传输数据的做法显然不是最佳的 。 一种更优的方式是：在数据工厂中一次性执行完全部运算再把数据传回 。

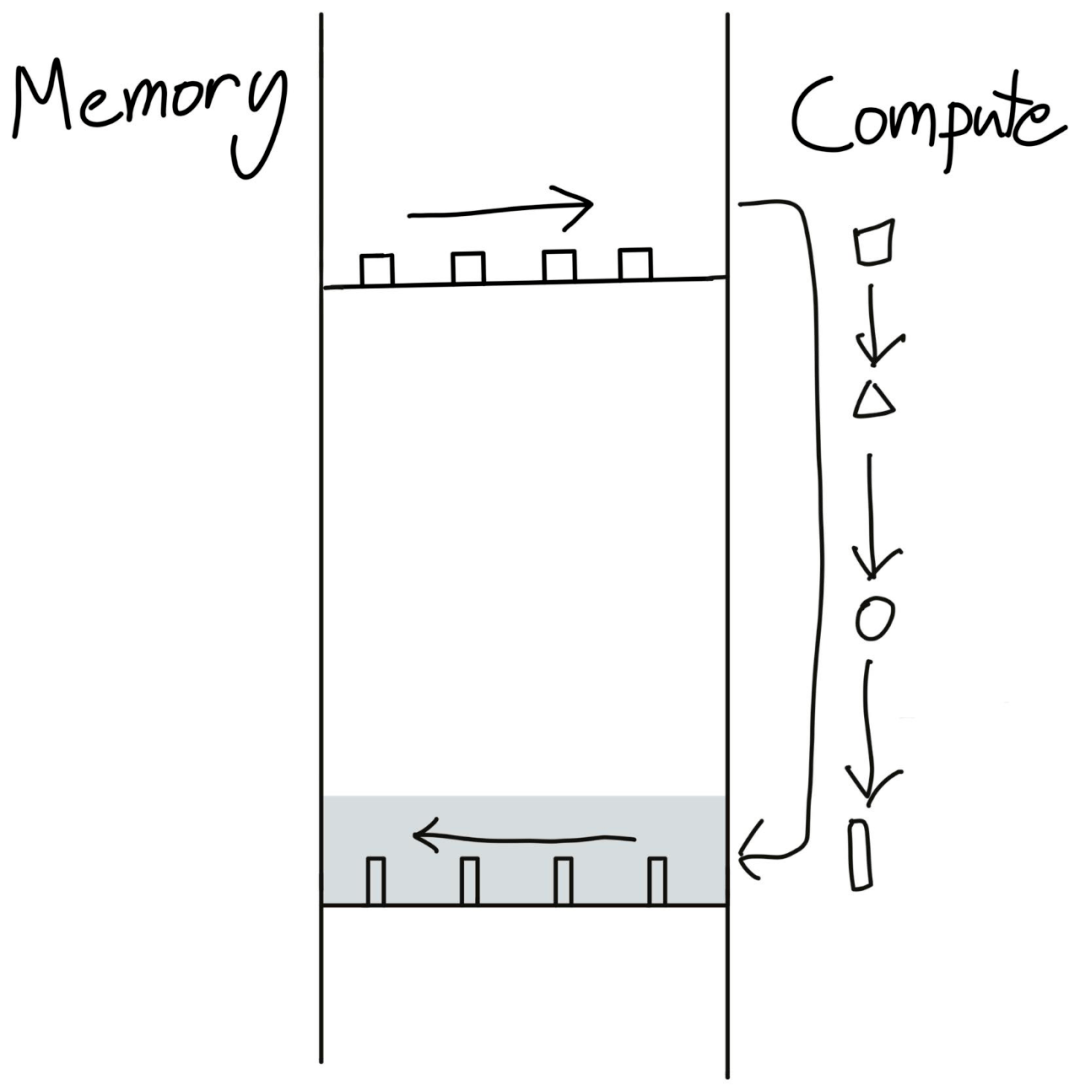
文章图片

这就是算子融合（operator fusion）—— 深度学习编译器中最重要的优化 。 简单地说 ， 这种方法不会为了再次读取而将数据写入全局内存 ， 而是通过一次执行多个计算来避免额外的内存访问 。
例如 ， 执行 x.cos ().cos () 运算 ， 写入内存的方式需要 4 次全局读写 。
x1 = x.cos() # Read from x in global memory, write to x1
x2 = x1.cos() # Read from x1 in global memory, write to x2
而算子融合只需要 2 次全局内存读写 ， 这样就实现了 2 倍加速 。
x2 = x.cos().cos() # Read from x in global memory, write to x2
但是这种做法也并不容易 ， 需要一些条件 。 首先 ， GPU 需要知道执行完当前运算后下一步会发生什么 ， 因此无法在 PyTorch 的 Eager 模式（一次运行一个运算符）下进行此优化 。 其次 ， 我们需要编写 CUDA 代码 ， 这也不是一件简单的事 。
并不是所有的算子融合都像逐点算子那样简单 。 你可以将逐点算子融合到归约（reduction）或矩阵乘法上 。 甚至矩阵乘法本身也可以被认为是一种融合了广播乘法（broadcasting multiply）和归约的运算 。
任何 2 个 PyTorch 算子都可以被融合 ， 从而节省了读取 / 写入全局内存的内存带宽成本 。 此外 ， 许多现有编译器通常可以执行「简单」的融合（例如 NVFuser 和 XLA） 。 然而 ， 更复杂的融合仍然需要人们手动编写 ， 因此如果你想尝试自己编写自定义 CUDA 内核 ， Triton 是一个很好的起点 。
令人惊讶的是 ， 融合后的 x.cos ().cos () 运算将花费几乎与单独调用 x.cos () 相同的时间 。 这就是为什么激活函数的成本几乎是一样的 ， 尽管 gelu 显然比 relu 包含更多的运算 。
因此 ， 重新实现 / 激活检查点会产生一些有趣的结果 。 从本质上讲 ， 进行额外的重新计算可能会导致更少的内存带宽 ， 从而减少运行时间 。 因此 ， 我们可以通过重新实现来减少内存占用和运行时间 ， 并在 AOTAutograd 中构建一个简洁的 min-cut 优化通道 。
推理内存带宽成本
对于简单的运算 ， 直接推理内存带宽是可行的 。 例如 ， A100 具有 1.5 TB / 秒的全局内存带宽 ， 可以执行 19.5 teraflops / 秒的计算 。 因此 ， 如果使用 32 位浮点数（即 4 字节） ， 你可以在 GPU 执行 20 万亿次运算的同时加载 4000 亿个数字 。
此外 ， 执行简单的一元运算（例如将张量 x2）实际上需要将张量写回全局内存 。
因此直到执行大约一百个一元运算之前 ， 更多的时间是花在了内存访问而不是实际计算上 。
如果你执行下面这个 PyTorch 函数：
def f(x: Tensor[N]):
for _ in range(repeat):
x = x * 2
return x
并使用融合编译器对其进行基准测试 ， 就可以计算每个 repeat 值的 FLOPS 和内存带宽 。 增大 repeat 值是在不增加内存访问的情况下增加计算量的简单方法 - 这也称为增加计算强度 （compute intensity) 。