好 ， 知道 光行差要求地球和以太之间有 相对运动 ， 并且它只精确到 v/c一阶 ， 无法测出这个相对运动的 具体速度 ，第一个实验就可以翻篇了 。
04-阿拉果的实验
光行差是个纯粹的天文观测 ， 它只涉及以太在 真空（空气）中的情况 ， 信息量有限 。 法国天文学家 阿拉果加了一块玻璃 ， 希望利用光在 不同介质中的 折射来获取更多的信息 。
阿拉果这个实验的原理有点绕 ， 大家要仔细理一理（理不清关系也不大 ， 知道最后的结论就行了） 。
你想啊 ， 如果地面上有一块 玻璃 ， 那 以太自然也会从玻璃中流过 。 那么 ， 如果有 一束光从空气射入玻璃 ， 你觉得会发生什么？
光在 以太中运动 ， 以太在 玻璃中流动 ， 那么 ，光在玻璃中的速度就应该是这两个速度的叠加 。 而速度又是一个 矢量 ， 不仅有大小 ， 还有 方向 ， 所以 光在玻璃中的速度就还跟这两个速度的 夹角有关 。
这就好比往河里仍一个皮球 ， 如果 顺着河水仍 ， 皮球的速度是最大的； 垂直河水仍 ， 皮球的速度会稍微小一点； 逆着河水仍 ， 皮球的速度就是最小的 。
很明显 ， 即便我仍皮球的速度 大小一样 ， 但只要 方向不同 ， 最终皮球的速度还是会不一样 。 同理 ， 光从不同方向射入流着以太的玻璃 ， 最后的速度也应该不一样 。
于是 ，阿拉果就转动望远镜 ， 让光线从 不同角度进入玻璃 。 试图通过改变光在玻璃中的 速度 ， 进而改变光在玻璃中的 折射率 ， 然后通过 折射定律观察到这种变化 。
考虑到有些 中小学生还不知道 折射率和 折射定律 ， 我这里非常简单的说一下 。
光从 一种介质进入 另一种介质时会发生 折射 。 如下图 ， 小鱼身上的光线其实是走 折线进入我们的眼睛的 ， 你顺着视线的方向是抓不到鱼的 ， 这就是一个典型的 折射现象 。 水杯中的筷子好像折断了 ， 也是因为光从水进入空气时发生了 折射 。

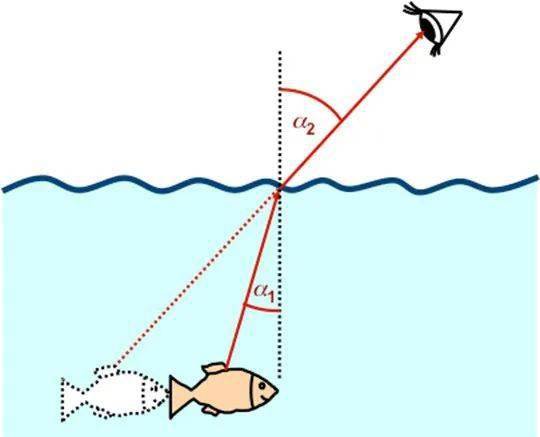
文章图片

折射的程度跟这两种介质的折射率有关 ， 而介质的 折射率 ， 就是光在 真空中的速度与 介质中速度的 比值 。
比如 ， 水的折射率是 1.33 ， 就是说光在真空中的速度是水中速度的 1.33倍 。 一般我们认为光在空气中的速度就等于真空光速 ， 也就是近似认为空气的折射率等于 1 。
光线发生折射时 ， 它的 入射角α1和 折射角α2的 正弦值与这两种介质的 折射率n1、n2之间有一个简单的比例关系 ， 这就是大名鼎鼎的 折射定律： n1sinθ1=n2sinθ2 。

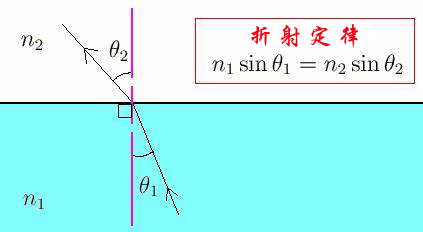
文章图片

于是 ， 当光线从不同方向射入玻璃时 ， 光在玻璃中的速度和 折射率都会发生变化 ，入射角和 折射角之间的关系也会发生改变 ， 而这是可以直接观察到的 。
但实验结果却让 阿拉果大为迷惑 ， 因为他发现 无论光从哪个方向进来 ， 他都观察不到玻璃的折射率有任何变化 。
也就是说 ， 我们改变入射光的方向时 ，光在玻璃中的速度好像并没有改变 ， 这跟说好的不一样啊！
为什么？ 阿拉果百思不得其解 ， 于是 ， 他选择求助场外观众 。 他于 1818年给波动说大佬 菲涅尔打了个电话 ， 不 ， 是写了封信 。
05-部分曳引假说
大佬就是大佬 ，菲涅尔收到阿拉果的来信之后 ， 很快就想到了一个解决办法 。
菲涅尔想 ，不同方向的光线进入玻璃后的速度应该是不一样的 ， 既然我们现在观测不到这种不一样 ， 那就肯定是还有某种机制把它抵消了 。