。
所以

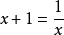
文章插图
。
由于


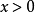
文章插图
解得


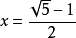
文章插图
所以极限是黄金分割比 。
它还有什么特性呢?
斐波那契数列的整除性与质数生成性
每3个连续的数中有且只有一个被2整除，
每4个连续的数中有且只有一个被3整除，
每5个连续的数中有且只有一个被5整除，
每6个连续的数中有且只有一个被8整除，
每7个连续的数中有且只有一个被13整除，
每8个连续的数中有且只有一个被21整除，
每9个连续的数中有且只有一个被34整除，
.......
我们看到第5、7、11、13、17、23位分别是质数：5，13，89，233，1597，28657（第19位不是）
斐波那契数列的质数无限多吗？
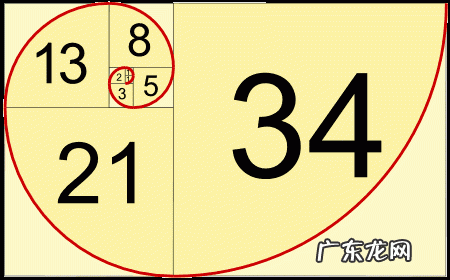
斐波那契数列与矩形面积的生成相关，由此可以导出一个斐波那契数列的一个性质 。


文章插图


文章插图
斐波那契数列前几项的平方和可以看做不同大小的正方形，由于斐波那契的递推公式，它们可以拼成一个大的矩形 。这样所有小正方形的面积之和等于大矩形的面积 。则可以得到如下的恒等式：


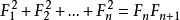
文章插图
杨辉三角中有斐波那契数学


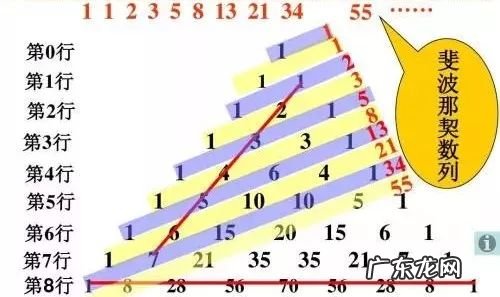
文章插图
自然界中“巧合”

自然界中的斐波那契数列和黄金分割点

斐波那契数列在自然科学的其他分支，有许多应用 。例如，树木的生长，由于新生的枝条，往往需要一段“休息”时间，供自身生长，而后才能萌发新枝 。所以，一株树苗在一段间隔，例如一年，以后长出一条新枝；第二年新枝“休息”，老枝依旧萌发；此后，老枝与“休息”过一年的枝同时萌发，当年生的新枝则次年“休息” 。这样，一株树木各个年份的枝桠数，便构成斐波那契数列 。这个规律，就是生物学上著名的“鲁德维格定律” 。
另外，观察延龄草、野玫瑰、南美血根草、大波斯菊、金凤花、耧斗菜、百合花、蝴蝶花的花瓣，可以发现它们花瓣数目具有斐波那契数：3、5、8、13、21、……


文章插图
其中百合花花瓣数目为3，梅花5瓣，飞燕草8瓣，万寿菊13瓣，向日葵21或34瓣，雏菊有34,55和89三个数目的花瓣 。
斐波那契螺旋：具有13条顺时针旋转和21条逆时针旋转的螺旋的蓟的头部
这些植物懂得斐波那契数列吗？应该并非如此，它们只是按照自然的规律才进化成这样 。这似乎是植物排列种子的“优化方式”，它能使所有种子具有差不多的大小却又疏密得当，不至于在圆心处挤了太多的种子而在圆周处却又稀稀拉拉 。叶子的生长方式也是如此，对于许多植物来说，每片叶子从中轴附近生长出来，为了在生长的过程中一直都能最佳地利用空间（要考虑到叶子是一片一片逐渐地生长出来，而不是一下子同时出现的），每片叶子和前一片叶子之间的角度应该是222.5度，这个角度称为“黄金角度”，因为它和整个圆周360度之比是黄金分割数0.618033989……的倒数，而这种生长方式就决定了斐波那契螺旋的产生 。向日葵的种子排列形成的斐波那契螺旋有时能达到89，甚至144条 。1992年，两位法国科学家通过对花瓣形成过程的计算机仿真实验，证实了在系统保持最低能量的状态下，花朵会以斐波那契数列长出花瓣 。

• 退货运费谁出流程,集运仓退货运费谁出
• 送别古诗长亭外,送别古诗长亭外
• 送女朋友礼物排行榜推荐,送女朋友礼物贵的推荐
• 现在学数控技术怎么样 数控技术专业属于哪类专业
• 页眉页脚怎么设置连续页数,页脚怎么连续设置页数
• 双十一阿里巴巴交易额 阿里双十一数据
• Have的第三人称单数怎么写 Have的第三人称单数是什么
• 什么牌子的数码产物好？数码品牌榜中榜
• 45岁生二胎有必要吗？多数持反对意见，细数高龄生子的优缺点 45岁生二胎的真实感受
• 2019四川高考分数线 四川高考分数线公布2020