不同于传统的强化学习,这些信息量巨大的奖励信号也被用作使控制器神经网络学着执行最大化累积奖励的动作的输入 。
14. 确定性策略梯度(1990)
在我 1990 年发表的论文 [AC90] 的「Augmenting the Algorithm by Temporal Difference Methods」一章中,我们也结合了用于预测累积奖励(可能是多维奖励,详见第十三章)的基于动态规划的时间差分方法 [TD] 以及基于梯度的世界预测模型(详见第十一章),从而计算单个控制网络的权值变化 。相关工作请参阅第 2.4 节介绍的 1991 年的后续工作 [PLAN3](以及类似的 [NAN1]) 。
25 年后,DeepMind 提出了该方法的一种变体「确定性策略梯度算法」(Deterministic Policy Gradient algorithm,DPG)[DPG][DDPG] 。
15. 用网络调整网络/合成梯度(1990)
1990 年,我提出了各种学着调整其它神经网络的神经网络 [NAN1] 。在这里,我将重点讨论 「循环神经网络中的局部监督学习方法」(An Approach to Local Supervised Learning in Recurrent Networks) 。待最小化的全局误差度量是循环神经网络的输出单元在一段时间内接收到的所有误差的总和 。在传统的基于时间的反向传播算法中(请参阅综述文章 [BPTT1-2]),每个单元都需要一个栈来记住过去的激活值,这些激活值被用于计算误差传播阶段权值变化的贡献 。
我没有让算法使用栈式的无限存储容量,而是引入了第二种自适应神经网络,该网络学着将循环神经网络的状态与相应的误差向量相关联 。这些局部估计的误差梯度(并非真实梯度)则会被用于调整 循环神经网络 [NAN1][NAN2][NAN3][NAN4] 。
不同于标准的反向传播,该方法在空间和时间上都是局部的 [BB1][NAN1] 。25 年后,DeepMind 将这种技术称为「合成梯度」(Synthetic Gradients)[NAN5] 。
16. 用于在线循环神经网络的时间复杂度为 O(n3) 的梯度计算
我们最初在 1987 年发表的用于完全循环连续运行的网络的固定大小的存储学习算法 [ROB],在每一个时间步需要 O(n^4) 的计算复杂度,其中 n 是非输入单元的数目 。我提出了一种方法来计算完全相同的梯度,它需要固定大小的与之前的算法同阶的存储空间 。但是,每个时间步的平均时间复杂度只有 O(n^3)[CUB1][CUB2] 。然而,这项工作并非没有意义,因为伟大的循环神经网络研究的先驱 Ron Williams 首先采用了这种方法 [CUB0]!
此外,1987 年,当我发表我当时认为是首篇关于遗传编程(GP,即自动演化的计算机程序 [GP1])的文论文时,也犯下了类似的错误,直到后来我才发现 Nichael Cramer 已经于 1985 年发表了 GP 算法 [GP0](而且在 1980 年,Stephen F. Smith 已经出了一种相关的方法,作为一个更大的系统的一部分 [GPA]) 。
自那以后,我一直尽我所能做到公正和诚信 。至少,我们 1987 年的论文 [GP1] 似乎是第一篇将 GP 用于带有循环结构以及可变大小的代码的论文,也是首次关于在逻辑编程语言中实现 GP 。
17. 深度神经「热交换器」(1990)
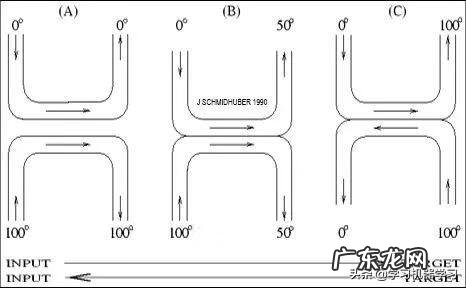
文章插图
「神经热交换器」(NHE)是一种用于深度多层神经网络的监督式学习方法,受启发于物理意义上的热交换器 。输入「加热」会经过许多连续层的转换,而目标则从深层管道的另一端进入并且进行「冷却」 。与反向传播不同,该方法完全是局部的,使其不需要进行并行计算也可以较快运行 。
自 1990 年 [NHE] 发表以来,我不定期地在各大学的演讲中会提到该方法,它的与亥姆霍兹机 (Helmholtz Machine) 关系密切 。同样,该方法的实验是由我杰出的学生 Sepp Hochreiter 完成的(详见第 3 章、第 4 章) 。
特别声明:本站内容均来自网友提供或互联网,仅供参考,请勿用于商业和其他非法用途。如果侵犯了您的权益请与我们联系,我们将在24小时内删除。
