文章插图
祖冲之
祖家是一个官宦人家，祖冲之的曾祖父在东晋时官至侍中、光禄大夫，相当于宰相和国策顾问之类 。他的祖父和父亲都在南朝做官，祖父是大匠卿，掌管宫室、宗庙、陵寝等的土木营建；父亲是奉朝请，这是闲散大官 。古时称春季的朝见为朝，秋季的朝见为请 。这个家族的历代成员，大多对天文历法颇有研究 。
相比之下，祖冲之担任过的官职较低，却在天文学和数学领域，乃至机械制造方面较其前辈取得了更为杰出的成就 。在刘宋时期，他曾担任南徐州（今镇江）的从事史，这是督促文书、察举非法的官职 。做过娄县（今苏州昆山）县令，也做过掌朝廷礼仪与传达使命的谒者仆射 。到了萧齐王朝，曾官至长水校尉，这是祖冲之一生担任的最高官职（四品） 。
从青年时代开始，祖冲之便对数学和天文学怀有浓厚兴趣，他曾在著作中自述说，自幼起“专功数术，搜炼古今” 。祖冲之把上古时起至他生活年代的各种文献资料搜罗来研究，同时亲自进行精密的测量和仔细的推算，也不把自己束缚在古人陈腐的思想中 。可以说，祖冲之批判地接受了前人的学术遗产，并勇于提出自己的新见解，这是古往今来一切杰出科学家共有的优良品质 。
在数学领域，祖冲之师承的是比他早两百多年的魏晋时期的刘徽，后者发明了计算圆周率的“割圆术”和计算球体积的方法 。由圆面积计算公式，容易得知，只要求得圆的面积，再除以半径的平方，即为圆周率 。而如何求圆面积，刘徽在《九章算术》的注释里这样写道，
割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体而无所失矣 。
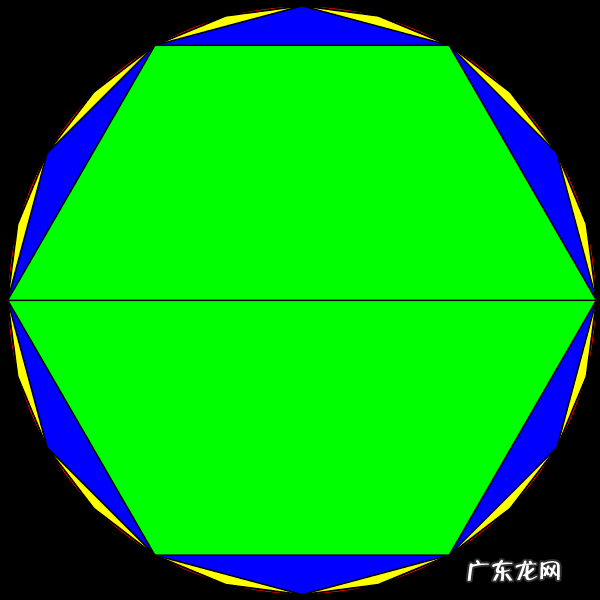
刘徽从圆内接正六边形开始计算面积，依次将边数加倍，求出内接正十二边形、正二十四边形、正四十八边形等等的面积 。随着边数的增加，内接正多边形的面积越来越接近圆的面积，圆面积和圆周率的精确度就越高 。

文章插图
刘徽的割圆术
在古代，包括中国和巴比伦在内的一些民族，都把3作为圆周率 。这方面，古埃及人的计算较为准确，他们得到的圆周率为3.1 。刘徽用他的割圆术，求得圆周率为3.14，这与古希腊数学家阿基米德算得的圆周率是一致的，后者比刘徽要早六个世纪 。学界普遍推测刘徽也算出了3.1416，但未有直接的证据 。
祖冲之计算出的圆周率范围为，
即精确到小数点后7位 。此外，他还得了被称为密率的这个分数的圆周率，虽然只精确到小数点后6位，却同样让人惊叹 。直到962年以后，祖冲之的圆周率才被阿拉伯统治下的波斯数学家卡西改进 。卡西利用了余弦函数的半角公式，简化了计算，精确到了小数点后17位 。而德国人奥托求得密率，则比祖冲之晚了一千多年 。
祖冲之的成就是如何取得的？没有任何史料流传下来，因为祖冲之的著作全部失传了，而记载圆周率值的《隋书》又没有具体交代 。由于当时只有刘徽的割圆术一种方法，因此我们只能猜测祖冲之用的是同样的方法 。那样的话，他需要算出圆内接正24576边形的面积，而密率（有日本学者建议称为祖率）的求得恐怕是借助于前辈天文学家何承天发明的“调日法” 。
3 球体积与大明历
相比圆的面积，球（古人称为立圆）体积的计算公式更富技巧 。在中国古典数学名著《九章算术》里，是按照以下比例公式来求球体积的
显而易见，正方形面积、圆面积和圆柱体面积这三项数据是比较容易求得的 。

• 涧下水命什么意思是什么
• 家里祖坟风水不好怎么办 祖先风水不好要怎么办
• 住宅风水化解 最好的住宅风水
• 风水中的局是怎么确定的 风水如何定局
• 宝鸭下田风水宝地 盘龙城风水宝地
• 窗户外有鸟窝风水上好么 窗台有鸟窝风水
• 大学生创业需要了解什么 如何了解大学生创业
• 姓翁的男孩取什么名字好
• 房子在电梯旁边风水 电梯挨着厨房的风水
• 西安最近为什么经常停电2021