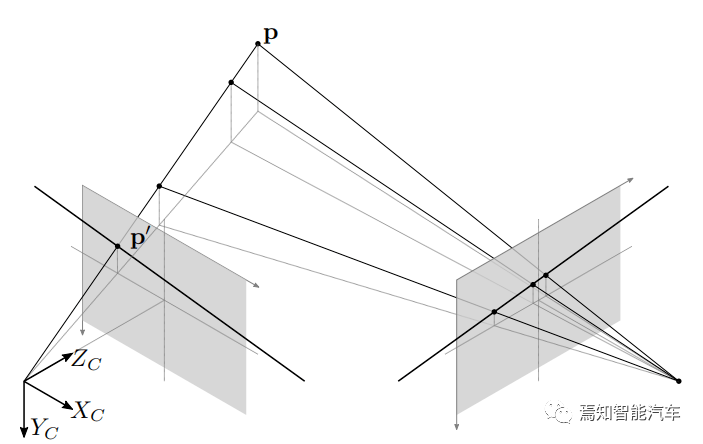
实际上 ， 通过物理排列来实现完美的相机对准是不可能的 。 两个相机之间的一般对齐方式如下图所示 。 点 p 投影到左侧相机图像平面上的点 p’ 。 这个点在右图像平面上的对应关系被限制在平面上绘制的水平基线上 。 事实上 ， 任何投影到左相机平面绘制线上的点都被限制为与右图像平面上的相应线重合 。 这些线被称为共轭极线 ， 两幅图像中各自的图像点在该极线上应该满足对极约束条件 ， 它们用于指导立体图像点对应的搜索过程范围 。

文章图片

图3 立体视觉测量提取算法示意图
对极约束的数学形式简单明了 ， 我们可以看出 ， 只要我们能够找出两幅图像之间的多组特征点关系 ， 就可以根据对极约束求出两幅图像之间的运动关系 。
接下来从数学角度描述一下对极约束 。
根据针孔相机模型,我们知道空间位置点P 在相机中的像素位置为p1 ， p2。 这里 K 为相机内参矩阵,R, t 为两个坐标系的相机运动(如果我们愿意,也可以写成代数形式) 。 如果使用齐次坐标,我们也可以把上式写成在乘以非零常数下成立的等式：
现在 ， 取:
这里的 x1 , x2 是两个像素点的归一化平面上的坐标 。 代入上式 ， 得:
两边同时乘以t的转置矩阵t^ ， 相当于两侧同时对t做外积：
然后 ， 两侧同时乘以 ， 那么
如上等式左侧 ，t^x2是一个与t和x2都垂直的向量（相当于对t和x2形成的平面做一条法线） ， 把它再和x2做内积时 ， 将得到0 ， 因此 ， 我们得到一个简洁的对极约束式子：
重新带入p1 ， p2 ， 得到另外一种表示形式
我们把对极约束数学表达式中的中间部分记为两个矩阵：基础矩阵(Fun-damental Matrix)F 和本质矩阵(Essential Matrix)E ， 可以进一步简化对极约束:
这里需要说明一下 ， 对于多目摄像头对环境信息的探测来说 ， 一般需要考虑两个摄像头必须保持一致的内参信息 。 其中包括焦距、主点、畸变量等 。 自动驾驶系统感知过程中 ， 经常会遇到一个比较经典的问题 ， 那就是如果采用两颗单目摄像头 ， 且该两颗摄像头并不是完全相同的 ， 甚至该两颗摄像头一个近焦广角 ， 一个远郊窄角 ， 是否可能在保证单目探测性能的同时实现更多的双目深度探测功能？
这里我们需要注意如果依赖对极约束 ， 实际上是将两个相机的投影矩阵相对于图像点进行了相应的位置约束 ， 而投影矩阵是内参与外参的乘积归一化 ， 所以从理论上讲 ， 无论两个相机内参和外参如何变化都应该满足对极约束 。 也就是说在其中一个相机中投影点一定能够在另一个相机中找到相应的投影位置 ， 这就使得两个点加上环境点所确定的三角形可以约束整个相机平面点的搜索范围 ， 从而通过三维重建可以完全确定环境点坐标位置 。
然而 ， 事实是在自动驾驶动态场景和高精度场景下 ， 该方案无法实现很好的探测能力 ， 因为同步性和一致性不太好 。 比如曝光起止时间无法做到很好的同步 ， 同时曝光区域也无法做到很好的同步 ， 这就会造成成像尺寸、清晰度、时间不一致 。 在后期 ， 可以通过微调来大致同步起始曝光时间 ， 但针对多种场景无法保证都可用 。 比如在通过对极约束解方程时 ， 对大目标（如大货车、大巴车、大卡车等）可以有一定量的深度测量 ， 而对小目标的精细测量却是不可行的 。
传感器外参标定
传感器融合的第一步是将来自各个子系统的测量值注册到一个共同的参考框架 ， 传感器之间几何偏移的不准确估计将导致错误配准 ， 从而影响感知性能 。 一般的 ， 描述传感器之间的对齐参数称为外部参数 。 本节将描述用于确定传感器外部参数的标定方法 。